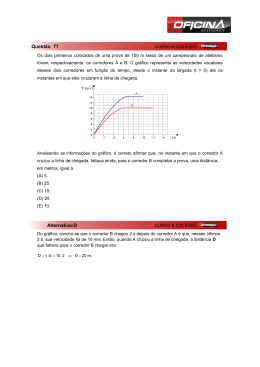
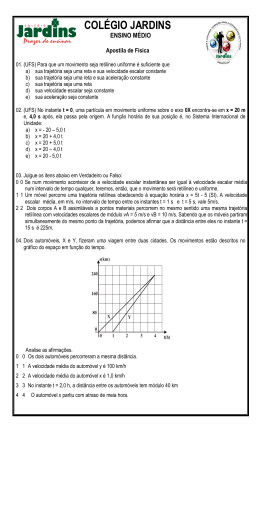
MECÂNICA
Entender o movimento é uma das metas das Física
A Mecânica estuda o movimento e as suas causas
A Mecânica Clássica se divide em:
1. Cinemática
2. Dinâmica
1
MECÂNICA CLÁSSICA
1. CINEMÁTICA estuda os movimentos sem levar em conta as causas do
movimento
2. DINAMICA
estuda as forças e os movimentos originados por essas forças
Força
2
1. CINEMÁTICA
1.1 Movimento em uma dimensão
O movimento representa uma mudança contínua da posição de um corpo
Todo movimento é definido em relação à um referencial
O movimento ao longo do eixo x
x
x
Utilizaremos o MODELO DE PARTÍCULA porque o tamanho do corpo real não tem
3
consequência na análise do seu movimento
Posição numa dimensão
Um corpo é localizado pela sua posição ao longo de um eixo orientado,
relativamente a um ponto de referência (o observador), em geral a
origem (x = 0)
-3
-2
-1
0
1
2
3
x (m)
4
Deslocamento numa dimensão
O deslocamento unidimensional de um objecto num intervalo de tempo
(t2 - t1) é a diferença entre a posição final (xf ) no instante tf e a posição
inicial (xi) no instante ti
Exemplo
Corrida de 100 m
deslocamento
 x = xf - xi
intervalo de tempo
 t = tf – ti
5
Exemplos
Exemplo 1. Corrida de 100 metros. O corredor parte de x1= 0 m para x2= 100 m. O
deslocamento do corredor é
x = xf - x1 = 100 m - 0 = 100 m
Exemplo 2. Uma pessoa andando se desloca do ponto x1= 200 m para x2= 100 m.
O deslocamento da pessoa é
x = xf - xi = 100 - 200 = - 100 m
6
Velocidade média
Temos a noção intuitiva de velocidade como sendo o espaço percorrido por um
corpo num certo tempo
t
x
x = xf - xi percorrida pela partícula
num intervalo de tempo t = tf - ti
A velocidade média é a distância
x
vm 
t
• Se x  0  vm  0 - movimento para a direita, ou no
sentido de crescimento de x
• Se x  0  vm  0 - movimento à esquerda, ou no
sentido de decréscimo de x)
A velocidade média nos dá informações sobre um intervalo de tempo
7
Exemplos
Exemplo 3. Na corrida de 100 m, o corredor nos primeiros 5.01 s, percorre 40 m e
depois percorre 60 m. O tempo total da corrida é de 10.5 s. Determinar : a) a velocidade
média do corredor até o instante de 5.01 s . b) a velocidade média do corredor após este
instante e até o final da corrida. c) a velocidade média do corredor em todo o intervalo
do tempo de duração da corrida.
a) De 0 a 5.01 s : x = xf - xi= 40 - 0 = 40 m
vm 
e
t = tf – ti= 5.01 s- 0 = 5.01 s
x 40 m

 8.0 m/s
t 5.01 s
b) De 5.01 a 10.5 s:
x = xf - xi= 100 m – 40 m = 60 m
vm 
e
t = tf – ti= 10.5 s - 5.01 s = 5.49 s
x 60 m

 10.9 m/s
t 5.49 s
c) Em todo o intervalo (de 0 a 10.5 s) :
x = xf - xi= 100 m – 0 = 100 m
vm 
x 100 m

 9.5 m/s
t 10.5 s
e
t = tf – ti= 10.5 s – 0 m = 10.5 s
8
Velocidade instantânea
x
É a velocidade que a partícula
tem a cada instante

x
dx
v  lim

t 0 t
dt
recta tangente à curva
t
A velocidade instantânea é a derivada da posição (x) em relação ao tempo (t)
Velocidade na direcção x:


v  vex

ex
t
x
9
Velocidade escalar média
A velocidade escalar média é uma forma diferente de descrever a rapidez com que uma
partícula se move. Ela envolve apenas a distância percorrida, independentemente da
direção e sentido:
vem
Em algumas situações
distância total

t
vem  vm
P


O
x
Entretanto, elas podem ser bastante diferentes
Exemplo: partícula parte de O, em ritmo constante,
atinge P e retorna a O, depois de decorrido um tempo
total
e ter percorrido uma distância total L

Neste caso:
vm  0
e
vem 
L
2

2

t
L

Velocidade escalar
A velocidade escalar é o módulo da velocidade; ela é destituída de qualquer indicação
de direção e sentido
Exemplo: O velocímetro de um carro marca a velocidade escalar instantânea e não a
10
velocidade, já que ele não pode determinar a direção e o sentido
Movimento rectilíneo uniforme
Chama-se movimento rectilíneo uniforme ao movimento em que a velocidade é constante
x  x0
v 
t  t0
x0
é a posição da partícula no instante inicial t = t0
v
é a velocidade com que a partícula se desloca
v
é constante
Para t0 = 0 temos a equação do movimento rectilíneo uniforme
x  x0  v t
Equação horária
11