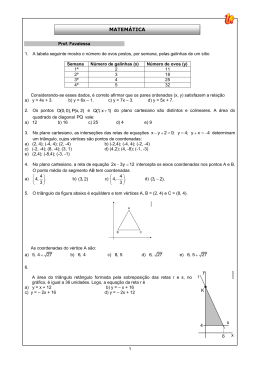
Questão 1: O gráfico abaixo representa um polinômio P(x) de
grau 4. Determine a soma dos coeficientes desse polinômio.
Representação gráfica das raízes de
uma Função Polinomial
 As raízes são as abscissas dos pontos de interseção da curva com o eixo x.
Uma raiz simples corta o eixo x sem
sofrer nenhuma deformação.
Uma raiz com multiplicidade par é
tangente ao eixo x.
x
x
Uma raiz com multiplicidade
ímpar intersecta o eixo x com
alguma deformação.
x
 Raízes: 1, 2 e –1; observe que
– 1 é dupla, pois o grau é 4.
 Termo independente:
P(0) = – 4
Forma Fatorada de um Polinômio
P(x) = a.(x – r1 ).(x – r2 ). ... .(x – rn )
P(x) = a.(x + 1)2.(x – 1).(x – 2)  P(x) = a.(x4 – x3 – 3x2 + x + 2)  P(0) = a.2 = – 4
a = – 2  P(x) = – 2x4 + 2 x3 + 6x2 – 2 x – 4
Soma = – 2 + 2 + 6 – 2 – 4 = ZERO
Lembrete: A soma dos coeficientes também pode ser
calculada por P(1) = – 2 + 2 + 6 – 2 – 4 = 0.
(Nesse caso, 1 é uma raiz simples.)
Questão 2: Determinar a equação da reta tangente à
circunferência x2 + y2 + 2x – 2y – 23 = 0 no ponto P = (3; 4).
Equação da Circunferência
Reduzida
(x – xC)2 + (y – yC)2 = R2
R
Normal
x2 + y2 + m.x + n.y + p = 0
C = (xC , yC )
 Completando os quadrados...
n
y C  2
m
xC  2
R

x 
C
2
  yC   p
2
 Equação da reta ...
B = (xB , yB)
A = (xA , yA)
 Equação da reta ...
y y A  yB
m

x x A  xB
... que passa por 2 pontos.
xA
yA
x
xB 1
yB 1  0
y 1
A.x  B.y  C  0
... a partir de um ponto e do
coeficiente angular.
y  y A  m.  x  x A 
y  m.x  n
Retas Paralelas
Retas Concorrentes
r
mr  ms
r
mr  ms
s
s
P
Sobre a equação reduzida y = m.x + n, lembre-se!
Retas Perpendiculares
Interseção com o Eixo y
y
r
1
mr  
ms
n
900
P
0
s
x
Propriedades importantes que envolvem
circunferências e retas
A
P
PA  PB
B
r  t
t
r
Na equação x2 + y2 + 2x – 2y – 23 = 0, temos:
t
2
yC  2  1
2
xC  2  1
C   1, 1
P
R
C
R

 1
2
 1   23   5
2
(x – (– 1))2 + (y – 1)2 = 52
(x + 1)2 + (y – 1)2 = 25
Essa equação é tangente à reta (t) no ponto P = (3, 4).
m
CP
y C  yP 1  4 3



xC  xP 1  3 4
CP  t
m
t

1

3
4
4

3
Agora, como conhecemos as coordenadas do ponto P e o coeficiente angular da reta (t), podemos escrever sua equação.
P   3, 4 
t
P
R
C
4
mt 
3
y  yP  m t .  x  x P 
4
y  4   . x  3 
3
4
y   x8
4x  3y  24  0
3
Questão 3: Resolva a equação |x2 – 4x| = 2x.
 Normalmente, esse tipo de questão aparece
logo no início da prova.
 Algumas vezes, há uma orientação explícita
para a construção dos gráficos num mesmo
sistema de referência cartesiano.
 As soluções dessa equação correspondem às
abscissas dos pontos de interseção entre os
gráficos.
f  x   x  4x
É uma função quadrática.
 A parábola tem a concavidade
voltada para cima (a > 0).
2
 Suas raízes são 0 e 4.
 Seu vértice é o ponto (2, 4).
b
x'  x"
xV 
ou x V 
2a
2

yV  f  xV  
4a
f  x   x2  4x
 Como o módulo está
aplicado apenas sobre f(x),
basta refletir a porção
negativa do gráfico em
relação ao eixo horizontal.
 Poderíamos, inclusive,
reescrever a função |f(x)|:
 x2  4x, x  0
f x   2
.
x  4x, x<0
f  x   x2  4x
f  x   x2  4x
g  x   2x
É uma função exponencial “clássica”.
 Não intersecta o eixo das
 A exponencial é crescente
abscissas.
(base > 1).
 Passa pelo ponto (0; 1).
 Sua imagem são os reais
positivos.
A solução da equação |x2 – 4x| = 2x é representada pelas
abscissas dos pontos de intersecção entre os dois gráficos.
Assim, a equação admite 3 soluções.
Questão 4: Na figura abaixo, o triângulo ABC é equilátero de
lado 8. Os segmentos AD, DE, EF, FB, BG, GH, HI, IC, CJ, JK,
KL e LA são congruentes. Determine o valor da área
sombreada.
TRIÂNGULO EQUILÁTERO
2
60o
L
a
60o
L
A=
h
L
3
4
a= h
3
L 3
h=
2
60o
L
ÁREA DE UM
TRIÂNGULO
ÁREA DE UM TRIÂNGULO
QUALQUER
a
h
b
h
h
b
b
ÁREA = BASE x ALTURA = b x h
2
2

b
ÁREA = a . b . sen
2
A  A ABC  2  A A  A B
2
B
6
A ABC
A A 
2
A
4
A
2
A B
82. 3

 16 3
4
4  2  sen60
2 3
2
6  2  sen60

3 3
2
4
Assim, podemos afirmar que A  16 3  2  2 3  3 3  9 3.