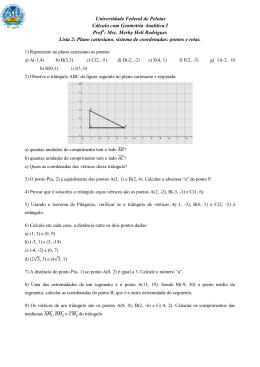
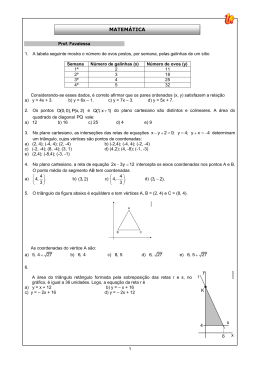
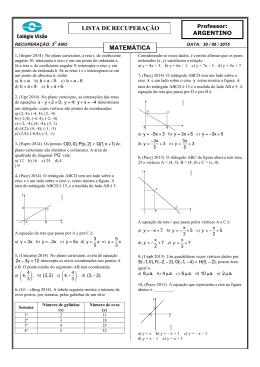
Lista de férias

Orientação de estudos:
1. Você deve rever as aulas iniciais sobre distância entre dois pontos e
coeficiente angular. Lembre-se que há duas maneiras para determinar o
coeficiente angular.
I.
Um ponto que pertence à reta e o ângulo de inclinação.
II.
Dois pontos pertencentes à reta.
Faça novamente os exercícios de aula e também os extras.
2. Do mesmo modo, você de rever as aulas sobre equação fundamental da
reta. Refazer os exercícios de aula e também os extras.
3. Agora faça os exercícios propostos 1 a 5.
4. A partir deste ponto você estudará alguns conceitos que dependerão da
equação fundamental da reta. Que são as posições relativas das retas
no plano cartesiano. A saber:
I.
Condição necessária e suficiente para que duas retas sejam
paralelas.
"Duas retas são paralelas quando seus coeficientes angulares
são iguais"
Refaça os exercícios da respectiva aula, os extras e em seguida faça os
exercícios propostos 6 a 10.
II.
Condição necessária e suficiente para que duas retas sejam
perpendiculares.
"Duas retas são perpendiculares quando o produto de seus
coeficientes angulares é igual a -1."
Refaça os exercícios da respectiva aula , os extras e em seguida faça os
exercícios propostos 11 a 15.
5. Para terminar estude as aulas sobre equação de circunferência reduzida
e normal.
Refaça os exercícios de aula e também as tarefas mínimas e
complementares. Isto será uma preparação para a prova trimestral.
Bons estudos e boas férias!
Exercícios propostos:
1. (UNICAMP-2011)A figura a seguir apresenta parte do mapa de uma cidade, no qual estão
identificadas a catedral, a prefeitura e a câmara de vereadores. Observe que o quadriculado não
representa os quarteirões da cidade, servindo apenas para a localização dos pontos e retas no plano
cartesiano.
Nessa cidade, a Avenida Brasil é formada pelos pontos equidistantes da catedral e da prefeitura,
enquanto a Avenida Juscelino Kubitschek (não mostrada no mapa) é formada pelos pontos
equidistantes da prefeitura e da câmara de vereadores.
Sabendo que a distância real entre a catedral e a prefeitura é de 500 m, podemos concluir que a
distância real, em linha reta, entre a catedral e a câmara de vereadores é de
a) 1500 m.
b) 500 5 m.
c) 1000 2 m.
d) 500 + 500 2 m.
2. (Enem 2010) A figura a seguir é a representação de uma região por meio de curvas de nível, que são
curvas fechadas representando a altitude da região, com relação ao nível do mar. As coordenadas estão
expressas em graus de acordo com a longitude, no eixo horizontal, e a latitude, no eixo vertical. A escala
em tons de cinza desenhada à direita está associada à altitude da região.
Um pequeno helicóptero usado para reconhecimento sobrevoa a região a partir do ponto X = (20; 60). O
helicóptero segue o percurso:
0,8°L  0,5°N  0,2° O  0,1° S  0,4° N  0,3 °L
De acordo com as orientações, o helicóptero pousou em um local cuja altitude é
a) menor ou igual a 200 m.
b) maior que 200 m e menor ou igual a 400 m.
c) maior que 400 m e menor ou igual a 600 m.
d) maior que 600 m e menor ou igual a 800 m.
e) maior que 800 m.
3. (Uerj 2002) No sistema de coordenadas cartesianas a seguir, está representado o triângulo ABC.
Em relação a esse triângulo,
a) demonstre que ele é retângulo;
b) calcule a sua área.
4. (Pucrj 1999) O valor de x para que os pontos (1,3), (-2,4), e (x,0) do plano sejam colineares é:
a) 8.
b) 9.
c) 11.
d) 10.
e) 5.
5. (Cesgranrio 1990) A distância entre os pontos M(4,-5) e N(-1,7) do plano x0y vale:
a) 14.
b) 13.
c) 12.
d) 9.
e) 8.
6. (G1 - cftmg 2014) A tabela seguinte mostra o número de ovos postos, por semana, pelas galinhas de
um sítio
Semana
1ª
2ª
3ª
4ª
Número de
galinhas (x)
2
3
4
5
Número de
ovos (y)
11
18
25
32
Considerando-se esses dados, é correto afirmar que os pares ordenados (x, y) satisfazem a relação
a) y = 4x + 3.
b) y = 6x – 1.
c) y = 7x – 3.
d) y = 5x + 7.
7. (Upe 2014) No plano cartesiano, as interseções das retas de equações x  y  2  0; y  4;
y  x  4 determinam um triângulo, cujos vértices são pontos de coordenadas:
a) (2, 4); (-4, 4); (2, -4)
b) (-2,4); (-4, 4); (-2, -4)
c) (-2, -4); (8, -4); (3, 1)
d) (4,2); (4, -8); (-1, -3)
e) (2,4); (-8,4); (-3, -1)
8. (Pucrj 2013) O triângulo da figura abaixo é equilátero e tem vértices A, B = (2, 4) e C = (8, 4).
As coordenadas do vértice A são:

a) 5, 4  27

b)  6, 4 
c)  8, 5 
 27 
e)  6, 5  27 
d) 6,
9. (Ufpr 2013) Considere as retas r e s representadas no plano cartesiano abaixo.
a) Escreva a equação da reta r.
b) Qual deve ser o coeficiente angular da reta s, de modo que ela divida o triângulo cinza em dois
triângulos com áreas iguais? Justifique sua resposta.
10. (Pucrj 2013) O triângulo ABC da figura abaixo tem área 25 e vértices A = (4, 5), B = (4, 0) e C = (c, 0).
A equação da reta r que passa pelos vértices A e C é:
a) y  x  7
x
5
3
x
c) y    5
2
x
d) y    7
2
x
e) y   7
3
11. (Cesgranrio 1990) Se as retas y + (x/2) + 4 = 0 e my + 2x + 12 = 0 são paralelas, então o coeficiente m
vale:
a) 2.
b) 3.
c) 4.
d) 5.
e) 6.
b) y  
12. (Cesgranrio 1993) As retas x + ay - 3 = 0 e 2x - y + 5 = 0 são paralelas, se a vale:
a) - 2
b) - 0,5
c) 0,5
d) 2
e) 8
13. (Ufmg 1994) Observe a figura.
Nessa figura, os pontos B, C e D são colineares, B = (2,3) e a área do triângulo OCD é o dobro da área do
paralelogramo OABC. Então, C é o ponto de coordenadas
 3
 5
 12 
b)  2, 
 5 
a)  2, 
c) (2, 1)
d) (3, 2)
e) (2, 2)
14. (Ufpe 1996) Na figura a seguir as retas r e s são paralelas, e a distância da origem (0,0) à reta s é
3 . A equação cartesiana da reta s é y=ax+b. Determine 6a2+4b2.
15. (Mackenzie 2001)
Na figura, a distância entre as retas paralelas r e s é
a) (17, -15)
b) (-8, 6)
c) (7, -3)
d) (-9, 5)
e) (3, 1)
2 e o triângulo OAB é isósceles. Um ponto de s é:
16. (Unesp 1990) A reta r é perpendicular à reta -3x + 4y - 5 = 0 e passa pelo ponto (1, 2). Determine os
pontos de r que distam 5 unidades do ponto (1, 2).
17. (Cesgranrio 1992) A equação da reta que contém o ponto A (1, 2) e é perpendicular à reta y=2x+3 é:
a) x + 2y - 5 = 0
b) 2x + y = 0
c) 2x + y - 4 = 0
d) x - 2y + 3 = 0
e) x + 3y - 7 = 0
18. (Ufmg 1995) A reta r é perpendicular à reta de equação 2x + y - 1 = 0 no ponto de abscissa -1.
A equação da reta r é
a) x - 2y + 7 = 0
b) 2x + y - 7 = 0
c) -x + 2y + 7 = 0
d) 2x + y + 7 = 0
e) x + 2y - 1 = 0
19. (Ufes 1996) Dados no plano cartesiano os pontos A = (-2, 1) e B = (0, 2), determine:
a) uma equação da reta que passa por A e B;
b) uma equação da reta que passa por A e é perpendicular ao segmento AB .
20. (Uel 1996) Considere os pontos A(0;0), B(2;3) e C(4;1).
O comprimento da altura do triângulo ABC, relativa ao lado BC , é
a)
2
3 2
2
2
2
c)
b)
5 2
2
e) 5 2
d)