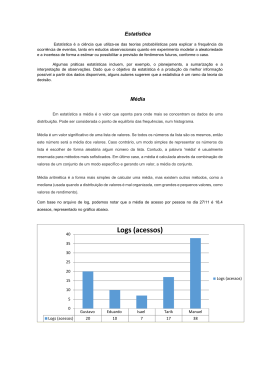
Estatística e Probabilidade




Medidas de tendência central
dispersão.
Média, mediana e moda.
Propriedades da curva normal
Exercícios.
e
medidas
de
•1. MEDIDAS ESTATÍSTICAS
•
• Amostras com variáveis quantitativas devem ser estudadas
de acordo com os seus descritores e distribuição.
• Os descritores ou medidas são basicamente:
• -Medidas de tendência central e medidas de dispersão.
• 1.1 Medidas de tendência central ou de posição.
• As medidas de tendência central mostram um valor ou
dado em torno do qual os dados da amostra agrupam-se:
• São a média, a mediana e a moda.
•
•
• 2. MEDIDAS DE TENDÊNCIA CENTRAL
• Média aritmética simples ou simplesmente média
•
• A média aritmética simples de um conjunto de valores é o valor
obtido somando-se todos eles e dividindo-se o total pelo número
de valores. É denotada (leia-se “x barra”)
•
• Observar que com dados agrupados deve-se usar a
multiplicação dos valores pela frequência ou seja: fx sobre o
somatório das frequências.
•
• E nos dados agrupados por intervalos de classe, xi e fi são os
valores do ponto médio e da freqüência absoluta da classe iésima respectivamente.
• Média aritmética simples ou simplesmente média
•
•Popriedade dos desvios:
• A soma dos desvios de cada valor com relação à média =
zero.
• Para dados agrupados em frequências simples:
•∑fd = ∑f (x- ) = 0
•
• Mediana
•
• A mediana é um valor central da série, divide a mesma em dois
subconjuntos iguais.
• Deve-se ordenar
decrescentes.
a
série
em
valores
crescentes
ou
• Para séries curtas, o que deve ser observado é a mediana
como média dos valores centrais se o n for par.
• O cálculo para séries longas é:
• mediana = (n+1) / 2
• Com dados grupados, a mediana corresponde à Fr = 0,5.
•
• Moda
• Moda ou moda de X, Mo, é o elemento mais freqüente no
conjunto.
•
• A moda é facilmente indicada na coluna de frequências simples.
• Para dados em intervalos de classe, há um intervalo modal, e a
moda é o ponto médio deste intervalo.
• No histograma, a moda são os picos da distribuição.
• Distribuições bimodais ou polimodais (vários picos) indicam
forte assimetria, afastamento da normalidade ou mistura de
amostras.
• Calcular a média, mediana e indicar a moda dos dados
referentes às medidas das conchas, escolhendo uma das
variáveis, CAC, LAC ou PC.
•3. MEDIDAS de dispersão.
• As medidas de dispersão revelam a variabilidade dos dados.
• Exceto a amplitude, mostram o grau de afastamento dos
valores observados em relação aos valores representativos
centrais.
• - Amplitude total: diferença entre os valores extremos da série.
• Variância e desvio padrão:
• Variância é a quantidade de desvios de cada valor em relação à
média. Tem os símbolos δ2 para dados populacionais ou s2 para
dados amostrais.
• O desvio padrão, δ ou s, é a raiz quadrada da variância. É
uma medida de dispersão apresentada na mesma unidade de
mensuração de x, lembrando que na variância os valores são
considerados como o seu quadrado.
• Fórmulas para a variância e desvio padrão:
•δ2 = ∑ (x-µ) 2
•
n
• µ = média da população.
• Ver fórmulas alternativas para amostras no livro, como:
• s2 = ∑ (x- ) 2
•
n-1
•
•
O desvio padrão, δ ou s, é a raiz quadrada da variância:
n-1
-1
• Coeficiente de variação:
• Trata-se de uma medida de dispersão, útil para a comparação
da variabilidade em séries diferentes, que apresentam variáveis
distintas. É dado por Cv ou pelo Cv%
s
•
• Idealmente uma amostra deve ter uma Cv baixo, refletindo
pouca variação dos dados com relação à média. Utiliza-se uma
aproximação do Cv a 20% ou menos da média para observar-se
esta característica. Em amostragens aleatórias esta relação pode
ser usada para uma aproximação do tamanho da amostra, desde
que esta tenha distribuição normal.
• Calcular a variância, desvio padrão e coeficiente de variação
referentes às medidas das conchas, escolhendo uma das
variáveis, CAC, LAC ou PC.
•4. AS DISTRIBUIÇÕES NORMAIS, A CURVA NORMAL OU
CURVA DE GAUSS.
•
• As populações descritas com variáveis quantitativas tem uma
tendência à distribuição normal, o que significa que os seus
histogramas apresentarão um desenho em forma de sino. Os
valores extremos coincidem com as abas do sino. Estes
diagramas em forma de sino foram descobertos e estudados por
Gauss, daí o termo curva de Gauss (matemático alemão 19771855).
• As amostras destas populações terão também distribuição
normal.
•
•4.1 PROPRIEDADES DA CURVA NORMAL.
•
•
2,5%
• A curva é simétrica.
• A média coincide com a ordenada máxima; a média coincide
com a mediana e moda (simetria); Curvas assimétricas ou
achatadas não mantém as mesmas derivações da normal.
• Tem dois pontos de inflexão que correspondem a 1 desvio
padrão (δ) acima e abaixo da média. Este limite corresponde a
68% dos valores de x, ou da população em estudo.
•4.1 PROPRIEDADES DA CURVA NORMAL.
•
•
2,5%
•
• Aproximadamente 95% da população situa-se entre µ-2 δ e µ+2
δ; Cerca de 99,7% dos valores se forem 3δ.
•4.2 A CURVA NORMAL REDUZIDA
•
• A curva normal reduzida é uma distribuição teórica de valores
de X padronizados.
• A abcissa é chamada de linha ζ ou Z. Os valores são então de
uma variável hipotética chamada z.
• Nesta distribuição µ = 0 e δ = 1.
• A área entre z = -1 e z = +1 é 0,6826. As áreas entre µ e
qualquer valor de z são informadas em tabelas como a A1.
•4.2 A CURVA NORMAL REDUZIDA
•
•
• A área que corresponde a valores de z entre -1,96 e + 1,96, é
de 0,4750 + 0,4750 = 0,95.
• Entre -2.58 e +2.58 é = 0,9902
• Realizar os exercícios referentes aos exemplos do livro 1, 2, 3.
•4.3 Procedimentos transformadores para distribuições sem
normalidade, assimétricas ou achatadas.
• As transformações mais usadas são para assimetrias à direita;
•
•
•
•
•
x´ = log x
x´ = √x
x´ = 1/x
Para assimetrias à esquerda:
• x´ = x2
•
•4.3 Procedimentos transformadores para distribuições sem
normalidade, assimétricas ou achatadas.
• O programa Biostat fornece testes de normalidade com base
nos parâmetros de simetria e curtose.
• Distribuições simétricas têm g1 próximo de 0, sendo menor do
que 0 inclinada para esquerda e maior do que 0 inclinada para a
direita.
• A curva normal é mesocúrtica, com um g2 próximo de 3. Um g2
maior do que 3, indica um excesso de observações nas
imediações da média e caudas, nas curvas assimétricas
leptocúrticas (skewed); um g2 menor do que 3 indica um excesso
de observações no ombros da curva, dita platicúrtica.
• Observar alguns exemplos.
•5. Aplicações da curva normal: áreas e proporções da curva.
•
• Transforma-se x em z da seguinte forma:
• z = x-µ
•
δ
• Exemplo 4.
• Na parte de exercícios, preparar:
• Exercícios 8, 9, 10, 11.
•
•5. Aplicações da curva normal: áreas e proporções da curva.
•
• As regiões de não significância dos valores com relação à
média, correspondem geralmente a valores de S 0-1,96 Z nos
dois lados da curva. Valores superiores a 1,96 correspondem a
2,5% de cada lado e compõe as áreas de significância das
diferenças, ou chamada área α (alfa). Utiliza-se geralmente dois
níveis de alfa: 0,05 (5%) - significante - e mais raramente 0,01
(1%) – muito significante.
2,5