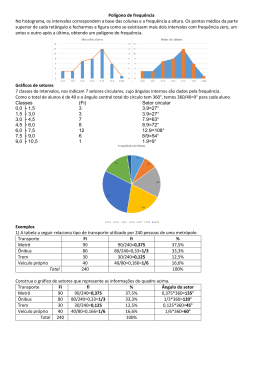
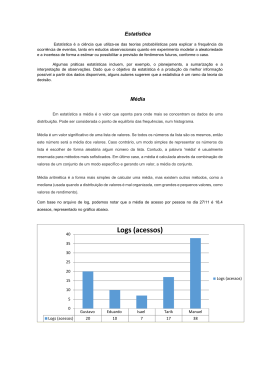
Medidas Descritivas
ESTATISTICA
Aula 5
PROF: CÉLIO SOUZA
1
Medidas de Posição –
descreve a agrupamento das amostras
MEDIDAS DE POSIÇÃO: agrupadas no inicio, no final ou no
meio.
Tendência Central- Média ( X), moda (Mo), mediana(Md)
Separatrizes (grupos iguais) - quartis (Q) e percentis (p)
MEDIDAS DE DISPERSÃO: descreve o afastamento das
amostras.
2
Amplitude (h), Variância ( S ) , Coeficiente de Variação (CV)
• Desvio-padrão (Dp)
• Intervalo inter-quartil.(IQ)
Medidas de Posição
Tendência Central
• Moda (Mo): valor mais freqüente na
amostra.
• Mediana (Md): valor central de um
conjunto de dados ordenados.
n
• Média:
X
x
X
• Onde:
é a média
n
n
•  x é a soma de todos os valores
• n = é o número de elementos da amostra
Medidas de posição & Assimetria
Distr. Simétrica
Moda
Mediana
Média
Assimetria
negativa
Moda
Média
Mediana
X<Md<Mo
Assimetria positiva
Moda
Média
Mediana
Mo<Md<X
Medidas de Posição
Percentis & Quartis
25% menores
observações
Q1
Q1: primeiro quartil
50% observações
centrais
Q2
Q2: segundo quartil = mediana
Q3: terceiro quartil
Q4: Quarto quartil
25% maiores
observações
Q3
Q4
Intervalo Interquartil
IQ  Q 3  Q 1
Medidas de Dispersão
• Amplitude: = max - min
n
• Variância:
S2 
• Desvio-padrão
(DP):
 x
i 1
 x
2
i
n 1
S 
• Coeficiente de Variação
(CV):
v a ri â n c i a 
S2
S
CV   100%
X
Medidas de Dispersão
• Amplitude = max - min
Grupo controle = 26,8 - 12,00 = 14,80
Grupo controle sem a observação = 20,9 - 12,00 = 8,90
Grupo B = 21,3 - 18,5 = 2,8
Características
• simples;
• Pode-se observar um grau de vareabilidade.
• Não considera a distribuição dos dados.
VARIÂNCIA
n
• Variância:
Grupo controle (A):
S2 
 x
i 1
 x
2
i
n1
S2 = 9,94
Grupo controle sem a observação:
S2 = 4,76
Grupo B:
S2= 0,67
Leva em consideração todas as variáveis da amostra.
Leva em consideração o desvio ao quadrado em torno
da média.
A variância ilustra homogeneidade entre dois grupos.
Medidas de Dispersão
• Desvio-padrão (s):
Grupo controle:
S
variância 
S
2
S = 3,15
Grupo controle sem a observação S = 2,18
Grupo B:
S = 0,82
Variância e desvio-padrão medem a dispersão “média” em
torno da média.
O DP mantém a unidade original dos dados.
COEFICIENTE DE VARIAÇÃO
• Coeficiente de Variação
(CV):
S
CV   100%
X
Características
Grupo A:
CV = 20,11%
Grupo B:
CV = 4,10%
•Útil para comparar a variabilidade de
dados expressos em unidades
distintas;
• Útil para comparar a variabilidade
de dados que são expressos nas
mesmas
unidades,
porém
apresentam valores muito distintos.
CV < 10 % = amostra homogênea
CV >10% <20 =
parcialmente Homogênea
> 20% = Heterogenia