Estatística
É a ciência que se utiliza das teorias probabilísticas para explicar a frequência da ocorrência de
eventos, tanto em estudos observacionais quanto em experimento modelar a aleatoriedade e a
incerteza de forma a estimar ou possibilitar a previsão de fenômenos futuros, conforme o caso.
Média
É o valor que aponta para onde mais se concentram os dados de uma distribuição, pode ser
considerada o ponto de equilíbrio das frequências, num histograma.
Média é um valor significativo de uma lista de valores. Se todos os números da lista são os
mesmos, então este número será a média dos valores. Caso contrário, um modo simples de
representar os números da lista é escolher de forma aleatória algum número da lista. Contudo, a
palavra 'média' é usualmente reservada para métodos mais sofisticados. Em último caso, a
média é calculada através da combinação de valores de um conjunto de um modo específico e
gerando um valor, a média do conjunto.
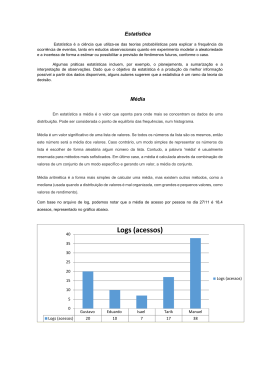
Segue abaixo os cálculos representando os dados do arquivo de log:
Com base no arquivo de log, podemos notar que a media de acesso nos dias 28/11, 29/11, 01/12
e 02/12 é de 29,75% e a média de acessos por IP é de 23,80%.
Mediana
É o valor numérico que separa a metade superior de uma amostra de dados, uma população ou
uma distribuição de probabilidade, a partir da metade inferior. A mediana de uma lista finita de
números pode ser encontrada por providenciar todas as observações do valor mais baixo para o
valor mais elevado e colheita do meio (por exemplo, a mediana de {3, 3, 5, 9, 11} é 5). Se
houver um número par de observações, então não existe um valor médio único, a mediana é,
então, geralmente definida como a média dos dois valores médios (a mediana de {3, 5, 7, 9} é
(5+7)/2 = 6), o que corresponde a interpretar a mediana como semi amplitudes totalmente
aparadas . A mediana é de importância central nas estatísticas robustas, já que é a estatística
mais resistente, ter um ponto de ruptura de 50%: enquanto não mais de metade dos dados está
contaminada, a mediana não vai dar um resultado arbitrariamente grande. A mediana é definida
apenas em dados unidimensionais encomendados, e é independente de qualquer distância
métrica. Uma média geométrica, por outro lado, é definida em qualquer número de dimensões.
Quanto à amostra do Log utilizado


Se utilizarmos como parâmetro de busca da mediana, o acesso por IPs, a
mediana seria o acesso de número 60, que foi realizado pelo IP 127.0.0.130, no
nome do Elcimar.
Se utilizarmos como parâmetro de busca da mediana, o acesso por dias, a
mediana seria, assim como descrito acima, o acesso de número 60, que
corresponderia ao 29/11.
Moda
É o valor que detém o maior número de observações, ou seja, o valor ou valores mais
frequentes, ou ainda "o valor que ocorre com maior frequência num conjunto de dados, isto é, o
valor mais comum".
O termo moda foi utilizado primeiramente em 1895 por Karl Pearson, sob influência do termo
moda referindo-se ao uso popular com o significado de objeto que se está usando muito no
tempo presente.
A moda não é necessariamente única, ao contrário da média ou da mediana. É especialmente
útil quando os valores ou observações não são numéricos, uma vez que a média e a mediana
podem não ser bem definidas.
Quanto à amostra do Log utilizado


Se utilizarmos como parâmetro de busca da moda, o acesso por IPs, esta seria o
IP 187.11.0.213, que foi realizado pelo Nickollas Soares, onde, ele acessou o
portal, um total de 37 vezes.
Se utilizarmos como parâmetro de busca da moda, o acesso por dias, esta seria, o
dia 28/11, pois, neste dia, obtivemos a quantidade de 48 acessos.
Variância
Na teoria da probabilidade e na estatística, a variância de uma variável aleatória é uma medida
da sua dispersão estatística, indicando quão longe em geral os seus valores se encontram do
valor esperado.
A variância de uma variável aleatória real é o seu segundo momento central e também o seu
segundo cumulante (os cumulante só diferem dos momentos centrais a partir do 4º grau,
inclusive). Sendo o seu valor o quadrado do Desvio Padrão.
A variância tem o objetivo de analisar o grau de variabilidade de determinadas situações,
através dela podemos perceber desempenhos iguais, muito próximos ou muito distantes. A
média aritmética pode ser usada para avaliar situações de forma geral, já a variância determina
de forma mais específica as possíveis variações, no intuito de não comprometer os resultados da
análise. Vamos, através de um exemplo, determinar a eficiência da variância.
Quanto à amostra do Log utilizado

A variância pode ser visualizada no aplicativo, sendo ela, utilizando como
parâmetro os acessos por IPs, ela é de 60,16. Porém, se utilizarmos como
parâmetro de busca os acessos por dia, ela será de 178,19.
Desvio Padrão
É a medida mais comum da dispersão estatística (representado pelo símbolo sigma, σ). Ele
mostra o quanto de variação ou "dispersão" existe em relação à média (ou valor esperado). Um
baixo desvio padrão indica que os dados tendem a estar próximos da média; um desvio padrão
alto indica que os dados estão espalhados por uma gama de valores.
O desvio padrão define-se como a raiz quadrada da variância. É definido desta forma de
maneira a dar-nos uma medida da dispersão que:


Seja um número não negativo;
Use a mesma unidade de medida dos dados fornecidos inicialmente.
Faz-se uma distinção entre o desvio padrão σ (sigma) do total de uma população ou de uma
variável aleatória, e o desvio padrão de um subconjunto em amostra.
O termo desvio padrão foi introduzido na estatística por Karl Pearson no seu livro de 1894:
"Sobre a dissecção de curvas de frequência assimétricas".
De acordo com o gráfico (quantidade de acessos dos dias) e com o arquivo de log, podemos
notar que o desvio padrão é 0,47, isto significa que os elementos estão bem próximos da media,
havendo um baixo grau de dispersão.
De acordo com o gráfico (quantidade de acesso por usuário) e com o arquivo de log, podemos
notar que o desvio padrão é 8,81, isto significa que os elementos estão distantes da media,
havendo um alto grau de dispersão.
Quanto à amostra do Log utilizado

Assim como a variância, o desvio padrão, também e referenciado no aplicativo,
sendo ele, utilizando como parâmetro de busca os acessos por IP, equivale á
7,76, e utilizando como parâmetros as datas, ele equivaleria a 13,35.
Coeficiente de Variação
O coeficiente de variação de Pearson é uma medida de dispersão relativa empregada para
estimar a precisão de experimentos e representa o desvio-padrão expresso como porcentagem da
média. Sua principal qualidade é a capacidade de comparação de distribuições diferentes.
O coeficiente de variação (CV) é obtido pela razão entre o desvio-padrão e a média. Indica-se a
variância por "S" (s elevado a 2). O desvio-padrão, calculado pela raiz quadrada da variância, é
representado por "S". Também considerado uma medida de dispersão, é relativo à média e,
como duas distribuições podem ter médias/valor médio diferente, o desvio-padrão dessas duas
distribuições não é comparável. A solução é usar o coeficiente de variação, que é igual ao
desvio-padrão dividido pela média.
Algumas vezes, o coeficiente de variação é ainda multiplicado por 100, passando a ser expresso
como percentagem. O coeficiente de variação em uma carteira de ativos serve como medida de
risco para cada unidade de ativo. O uso do coeficiente de variação é usualmente recomendado
para variáveis quantitativas do tipo razão (na qual exista um zero absoluto), tais como altura,
peso e velocidade.
Se a variável não é do tipo razão (ex.: temperatura em graus Célsius), o coeficiente de variação
poderá assumir valores negativos (ex.: caso a média seja negativa) e sua interpretação dependerá
do ponto de referência (ponto considerado como "0" na escala), levando a interpretações
equivocadas e relativas.
Quanto à amostra do Log utilizado

Assim como a variância e o desvio padrão, o coeficiente de variação, também
pode ser visualizado na aplicação, onde, utilziando como parâmetros de busca os
acessos por IP, o coeficiente seria de 32,59 %, e, utilizando como parâmetros os
acessos por dia, ele seria de 44,87%.
Probabilidade
A palavra probabilidade deriva do Latim probare (provar ou testar). Informalmente, provável é
uma das muitas palavras utilizadas para eventos incertos ou conhecidos, sendo também
substituído por algumas palavras como “sorte”, “risco”, “azar”, “incerteza”, “duvidoso”,
dependendo do contexto.
O estudo da probabilidade vem da necessidade de em certas situações, prevermos a
possibilidade de ocorrência de determinados fatos.
Ao começarmos o estudo da probabilidade, normalmente a primeira ideia que nos vem à mente
é a da sua utilização em jogos, mas podemos utilizá-lo em muitas outras áreas. Um bom
exemplo é na área comercial, onde um site de comércio eletrônico pode dela se utilizar, para
prever a possibilidade de fraude por parte de um possível comprador.
Distribuição Normal
A distribuição normal é uma das mais importantes distribuições da estatística, conhecida
também como Distribuição de Gauss ou Gaussiana. Foi primeiramente introduzida pelo
matemático Abraham de Moivre.
Além de descrever uma série de fenômenos físicos e financeiros, possui grande uso na
estatística inferencial. É inteiramente descrita por seus parâmetros de média e desvio padrão, ou
seja, conhecendo-se estes valores consegue-se determinar qualquer probabilidade em uma
distribuição Normal.
Um interessante uso da Distribuição Normal é que ela serve de aproximação para o cálculo de
outras distribuições quando o número de observações fica grande. Essa importante propriedade
provém do Teorema do Limite Central que diz que "toda soma de variáveis aleatórias
independentes de média finita e variância limitada é aproximadamente Normal, desde que o
número de termos da soma seja suficientemente grande" (ver o teorema para um enunciado mais
preciso).
A distribuição normal foi introduzida pela primeira vez por Abraham de Moivre em um artigo
no ano 1733, que foi reproduzido na segunda edição de seu The Doctrine of Chances (1738) no
contexto da aproximação de distribuições binomiais para grandes valores de n. Seu resultado foi
estendido por Laplace, em seu livro Analytical Theory of Probabilities (1812), e agora é
chamado o teorema de Moivre-Laplace.
Laplace usou a distribuição normal na análise de erros de experimentos. O importante método
dos quadrados mínimos foi introduzido por Legendre, em 1805. Gauss, que alegou ter usado o
método desde 1794, demonstrou-o rigorosamente em 1809 supondo uma distribuição normal
para os erros.
O nome "curva em forma de sino" ou "curva de sino" remonta a Esprit Jouffret que primeiro
utilizou o termo "superfície de sino" em 1872 para um normal bivariado com componentes
independentes (atentar que nem toda curva de sino é uma gaussiana). O nome "distribuição
normal" foi inventado independentemente por Charles S. Peirce, Francis Galton e Wilhelm
Lexis, por volta de 1875.