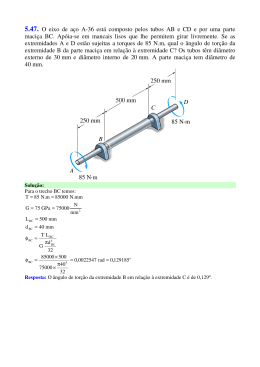
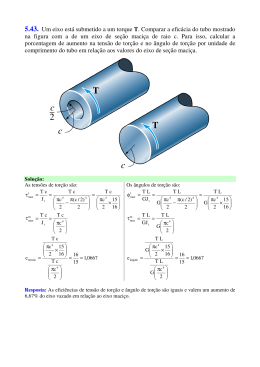
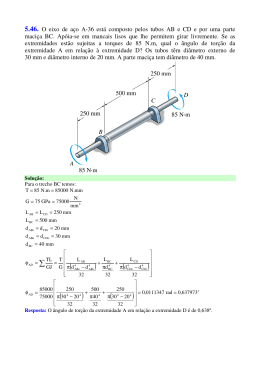
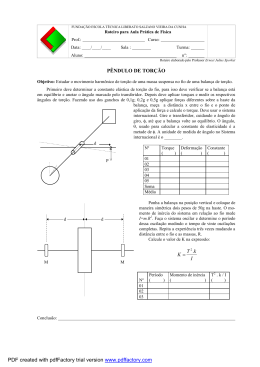
Ângulo de torção (φ):
Considerando eixo seção transversal circular, material homogêneo e comportase de maneira linear- elástica τ = Gγ
τ=
T ( x) ρ
J ( x)
TL
φ=
JG
Convenção de sinais: regra da mão direita – torque a ângulo são positivos se a
direção indicada do polegar afastar-se do eixo quando os dedos são fechados
para indica a tendência da rotação.
35) As engrenagens acopladas ao eixo de aço com uma das extremidades fixa
estão sujeitas aos torques mostrados na figura. Supondo que o módulo de
elasticidade de cisalhamento seja G=80 GPa e o eixo tenha diâmetro de 14 mm,
determinar o deslocamento do dente P da engrenagem A. O eixo gira livremente
no mancal em B.
36) As extremidades estriadas e as engrenagens acopladas ao eixo de aço A-36
estão submetidas aos torques mostrados. Determinar o ângulo de torção da
extremidade B em relação à extremidade A. O eixo tem diâmetro de 40 mm.
Elemento estaticamente indeterminado carregados com
torque
φA B = 0
37) O eixo de aço maciço tem diâmetro de 20 mm. Se for submetido aos dois
torques, quais serão as reações nos apoios fixos A e B?
Eixos sólidos não-circulares
38) O eixo de alumínio 6061-T6 tem área
da seção transversal na forma de um
triângulo eqüilátero. Determinar o maior
torque T que pode ser aplicado na
extremidade do eixo se a tensão de
cisalhamento admissível é de 8 ksi e o
angulo de torção em sua extremidade é
limitado a 0,02 rad. Qual torque poderia
ser aplicado a um eixo de seção
transversal circular feito da mesma
quantidade de material?
Concentração de tensão
τ máx
Tc
=K
J
39) O eixo em degrau mostrado na
figura é apoiado por mancais em A e B.
Determinar a tensão máxima nele
desenvolvida devido aos torques
aplicados. A curva de concordância na
junção de cada eixo tem raio r = 6 mm.