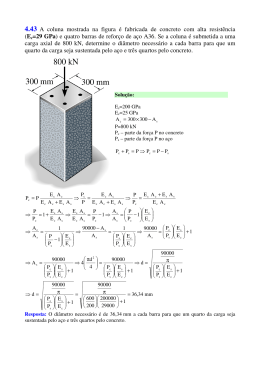
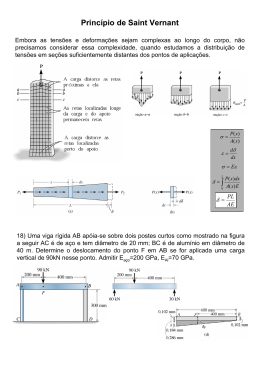
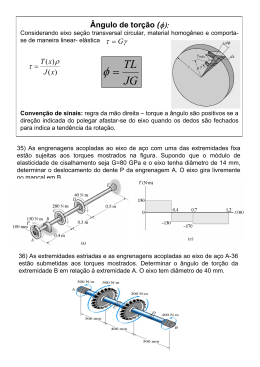
ENG 1007 – INTRODUÇÃO À MECÂNICA DOS SÓLIDOS
Segunda prova – turma A
29/04/2014
a
1 Questão (2,5 pontos)
Duas engrenagens estão aplicadas a dois eixos de aço (G=84GPa) de 50 mm de diâmetro, como
mostrado na figura. A engrenagem em B tem diâmetro de 200 mm; a engrenagem em C tem 400 mm de
diâmetro. A extremidade D está engastada, não podendo girar.
a) Calcular o ângulo de rotação da seção A se nesta seção é aplicado um torque de 560 Nm.
b) Qual é a máxima tensão de cisalhamento?
Tr
J
πd4
J=
32
T ∆L
∆ϕ =
GJ
τ=
Resposta:
Quando eixos são ligados por engrenagens, como mostrado, o torque é proporcional à relação entre os
diâmetros das engrenagens, já que as forças atuantes entre os dentes das engrenagens são iguais.
Dado: torque no trecho AB = 560NM . Calculado: torque no trecho CD = 560
Resposta:
1120 Nm × 3m
= 0,0652rad
84 × 10 Pa × π × 0,0254 m 4 / 2
Portanto, ∆ϕ AD = ∆ϕ AB + ∆ϕCD = 0,1304rad
1120 Nm × 0,025m
b) τ máx =
= 45,633MPa
π × 0,0254 m 4 / 2
a) ∆ϕCD =
9
∆ϕ AB =
400
= 1120 Nm .
200
560 Nm × 6m
= 0,0652rad
84 × 10 Pa × π × 0,0254 m 4 / 2
9
2a Questão (2,5 pontos)
A bomba ilustrada abaixo opera com um motor que tem potência de 85 W. Supondo que o impulsor em
B esteja girando a 150 revoluções por minuto, determinar a tensão de cisalhamento máxima
desenvolvida em A, localizada no eixo de transmissão, que tem 20 mm de diâmetro.
T ( x ) Gρ
P = 2π nT ; τ ( x, ρ ) =
r( x )
2π ∫ G ρ 3d ρ
0
Resposta:
T = 85 ( 2π × 150 / 60 ) = 5, 411Nm
τ máx =
5, 411 × 0,01
π × 0,014 / 2
= 3, 445MPa
3a Questão (2,5 pontos)
O tubo fino da figura abaixo é feito de três chapas de aço (G = 84 GPa), com 5 mm de espessura cada,
de modo que tem seção transversal triangular de 200 mm de lado, em média.
Determinar o torque máximo T ao qual o tubo pode ser submetido se a tensão de cisalhamento
admissível é τ adm = 90 MPa e ele está restrito a uma torção de não mais que ϕ = 2 ×10−3 rad .
τ=
T
2A m t
dϕ =
T ⌠ ds

dx
4A 2m G ⌡Cm t
Resposta:
Am = 0, 22 3 / 4 = 0,01732m2
Cm = 3 × 0, 2 = 0,6 m
T
τ máx =
≤ 90MPa
2 × 0,01732m 2 × 0,005m
T × 3m × 0,6m
∆ϕ =
≤ 2 × 10−3 rad
4 × 0,017322 m4 × 84GPa × 0,005m
⇒ T ≤ 15,59kNm
⇒ T ≤ 560 Nm .
Portanto, Tmáx = 560 Nm
4a Questão (2,5 pontos)
O eixo composto de aço e alumínio da figura está submetido aos torques indicados, em que T = 40
kN.m. O eixo consiste em um segmento AB todo de aço, acoplado a outro segmento BC com núcleo de
alumínio encamisado por um tubo vazado de aço, que por sua vez se acopla ao tubo de parede fina de
aço CD. O comprimento de cada segmento é L = 1 m, os raios são r1 = 10 cm e r2 = 8 cm e a espessura
é t = 4 mm. Os módulos de elasticidade transversal do aço e do alumínio são Gaço = 84 GPa e Gal = 28
GPa. Calcular
a) a rotação da extremidade D;
b) as tensões máximas que ocorrem no trecho BC para o aço e o alumínio.
dϕ
T ( x)
= r( x)
r1 = 10 cm
t = 4 mm
alumínio r2 = 8 cm
dx
aço
2π ∫ Gρ 3d ρ
T
T
0
3T
T ( x)Gρ
τ ( ρ , x) = r ( x )
C
A
B
D
L=1m
L=1m
L=1m
2π ∫ Gρ 3d ρ
L
L
L
L
0
Resposta
Diagrama de torques:
3T
4T
T
Rotação da extremidade D;

40 × 1 
3
4
1
ϕ AD =
+
+

 = 0,0447 rad
6
4
3
4
4
4
28 × 10 π  3 × 0,1 / 2 ( 0,08 + 3(0,1 − 0,08 ) ) / 2 2 × 3 × 0,1 × 0,004 


Tensão máxima no alumínio no trecho BC:
4 × 40 × 28 × 106 × 0,08
τ alBC =
= 37,366 MPa
28 × 106 ( 0,084 + 3(0,14 − 0,084 ) ) π / 2
Tensão máxima no aço no trecho BC:
4 × 40 × 84 × 106 × 0,1
BC
τ aço
=
= 140,122 MPa
28 × 106 ( 0,084 + 3(0,14 − 0,084 ) ) π / 2