Lista de exercícios para a final 01 Determinem as cargas internas resultantes que agem na seção transversal que passa pelo ponto B. 02 A viga suporta a carga distribuída mostrada. Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto C e D. Considere que as reações nos apoios A e B sejam verticais. 03 A viga rígida é sustentada por um pino A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD. 04 O parafuso de 8 mm de diâmetro é feito de liga de alumínio e está instalado em uma luva de magnésio com diâmetro interno de 12 mm e diâmetro externo de 20 mm. Se os comprimentos originais do parafuso e da luva forem 80 mm e 50 mm, respectivamente, determine as deformações na luva e no parafuso se a porca do parafuso for apertada de tal modo que a tensão no parafuso seja de 8 kN. Considere que o material em A é rígido Eal= 70 GPa, Emg= 45 GPa. 05 o arganéu da âncora suporta uma força de cabo de 3 kN. Se o pino tiver diâmetro de 6 mm, determine a tensão média de cisalhamento no pino. 06 A junta está presa por dois parafusos. Determine o diâmetro exigido pAula
ara os 6
parafusos se a tensão de reptura por cisalhamento para os parafusos for Trup = 350 MPa. Use um fator de segurança para cisalhamento FS= 2,5. !9(*@A@1&'B'
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercício 1
ST'U'+%@"')"1+#-,"'*-'V5%#-'+&)'%)',2W)&+#"'2*+&#*"',&'XY'
1) O tubo mostrado na figura tem um diâmetro interno de 80 mm e diâmetro
))'&',2W)&+#"'&3+&#*"',&'SYY'))6'7%/"*,"'$%&'1%-'
externo de 100 mm. Supondo que sua extremidade seja apertada
contra o
&3+#&)2,-,&'1&9-'-/&#+-,-'."*+#-'"'-/"2"'&)'E&/"#')&2"',&'
apoio
em A Spor
meio de um torquímetro em B, determinar a tensão de
A h
aste p
lástica d
e a
crílico t
em 2
00 m
m d
e c
omprimento e
1
5 m
m d
e d
iâmetro. e 07 %)'+"#$%;)&+#"'&)'F=',&+&#)2*-#'-'+&*1?"',&'.21-4B-)&*+"'
cisalhamento desenvolvida no material nas paredes interna e externa ao
uma carga axial de 300 n for aplicada a ela, determine a mudança em seu longo da parte central do tubo quando são aplicadas forças de 80 N ao
,&1&*:"4:2,-'*"')-+&#2-4'*-1'/-#&,&1'2*+&#*-'&'&3+&#*-'-"'
comprimento e em seu diâmetro Ep = 2,70 GPa, Vp = 0,4. torquímetro.
4"*5"',-'/-#+&'.&*+#-4',"'+%@"'$%-*,"'1?"'-/42.-,-1'8"#0-1'
,&'XY'Z'-"'+"#$%;)&+#"6'
de 75 mm e externo de 95 mm. 08 O tubo mostrado na figura tem diâmetro interno Se sua extremidade for apertada contra o apoio em A usando-­‐se uma chave em B, determine a tensão de cisalhamento desenvolvida no material nas paredes interna e externa ao longo da porção central do tubo quando são aplicadas forças de 80 N à chave. !"#$%&'()*+",#)&-%&!(".,&&&/&&&0"#$12"#)#,34(5.67%2#8%9"&
:+,.,6;)2.(&*#,&<(6+".(.,&
Resistência dos Materiais
5.5. O eixo maciço de 30 mm de diâmetro é usado para transmitir os torques
09 aplicados às engrenagens. Determinar a tensão de cisalhamento desenvolvida nos
pontos C e D do eixo. Indicar a tensão de cisalhamento nos elementos de volume
Prof. MSc. Luiz Eduardo Miranda J. Ro
Aula
5
localizados
nesses pontos.
As extremidades estriadas e as engrenagens acopladas ao eixo de aço A-­‐36 estão submetidas aos torques mostrados. Determinar o ângulo de torção da extremidade B em relação à extremidade A. O eixo tem diâmetro de 54 mm <'*#-.-(0%F%
Exercício 1
•  VO"W"9*2?$2#*"7*1#.'+*"2'"@3$.'"9*2141#,"+,"$7"#$%*"+,"
1) O conjunto
mostrado na figura consiste de um tubo de alumínio AB com área da
'&$7X24*"#%"9*7"6.,'"+'"1,()*"#.'21>,.1'&"+,"YZZ"77[A"
seção transversal
de 400 mm². Uma haste de aço de 10 mm de diâmetro est
E7'"='1#,"+,"'(*"+,"VZ"77"+,"+4M7,#.*",1#6"'9*-&'+'"'"
acoplada a um
colar rígido que passa através do tubo. Se for aplicada uma carga de
tração de 80 $7"9*&'.".X34+*"G$,"-'11'"'#.'>C1"+*"#$%*A"U,"/*."'-&49'+'"
kN à haste, qual será o deslocamento da extremidade C?
$7'"9'.3'"+,"#.'()*"+,"\Z"I]"^"='1#,<"G$'&"1,.6"*"
Supor que Eaço
= 200 GPa e Eal = 70 GPa.
+,1&*9'7,2#*"+'",;#.,74+'+,"&_"
•  U$-*."G$,">(C#&L"[ZZ"`B'",">(5&L"aZ"`B'A"
10 Solução:
O conjunto mostrado na figura é composto por um tubo de alumínio AB com área Para o ponto C temos:
2
de seção transversal de 320 mm . Uma barra de aço com 12 mm de está TCd=iâmetro −300 + 500
= 200 N.m = 200000 N.mm
acoplada a um colar rígido e passa pelo tubo. Se uma carga de Tração P mm
= 80 kN for d = 30
TC Cdonsidere T dO eixo
16 TdeC aço16A-36
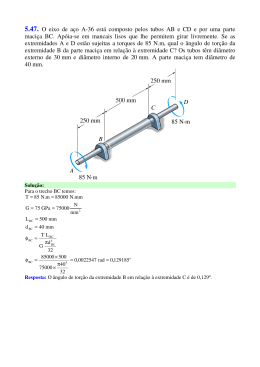
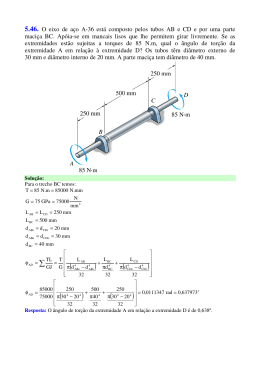
5.46.
está composto pelos
× 200000
N tubos AB e CD e por uma parte
aplicada à barra, determine o deslocamento da extremidade C da bτarra. =
= C 4 BC.
= Apóia-se
= em mancais
= lisos
37,7256
C
que mm
lhe 2permitem girar livremente. Se as
2 J maciça
πd
πd 3
π × (30) 3
E(aço) = 200 GPa e E(al) = 70 GPa. 2
extremidades
estão sujeitas a torques de 85 N.m, qual o ângulo de torção da
32
extremidade
A em relação à extremidade D? Os tubos têm diâmetro externo de
30 mm e diâmetro interno de 20 mm. A parte maciça tem diâmetro de 40 mm.
11 TC
!"#$%&'()*+",#)&-%&!(".,&&&/&&&0"#$12"#)#,34(5.67%2#8%9"&
O eixo de aço A-­‐36 está composto pelos tubos AB e CD e por uma parte maciça BC. Apoia-­‐se em mancais lisos que lhe permitem girar livremente. Se as extremidades estão sujeitas a torques de 85 N.m, qual o ângulo de torção da extremidade B em relação à extremidade C? Os tubos têm diâmetro externo de 36 mm e odponto
iâmetro Para
D temos:
TD = −300 + 500 + 200 = 400 N.m = 400000 N.mm
interno de 22 mm. A parte maciça tem diâmetro de 44 mm. :+,.,6;)2.(&*#,&<(6+".(.,&
!F(*4G4;&'H'
Resistência dos M
QC"O3"'.<$'.0<'.3"07%#/0)03"0%"',-%")'"01%"7%+"*+0")03"
'-($'+,)0)'3"P-0"'3(6%"3*&',(03"0%3"(%$4*'3"+%3($0)%3".0"
T d T d 16 T
16 × 400000
N
τ =
=
=
=
= 75,4512
2 J P<*$0="N*#%.)%"4*'"%"+H)*/%")'"'/0357,)0)'")'"
πd
πd
π × (30)
mm
TD
2
7,30/I0+'.(%"3'&0"$%?"RS"TU0"'"%"',-%"('.I0"),;+'($%")'"
32
QV"++:")'('$+,.0$"%")'3/%70+'.(%")%")'.('"&%)0"
Resposta: '.<$'.0<'+"'="!"',-%"<,$0"/,L$'+'.('".%"+0.70/"'+"(="
As tensões máximas de cisalhamento nos pontos C e D são: 37,7 MPa e 75,5 MPa,
d = 30 mm
D
D
D
12 D
3
4
3
2
respectivamente.
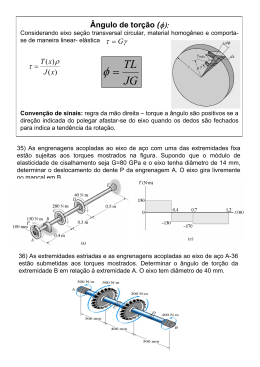
As engrenagens acopladas ao eixo de aço com uma das extremidades fixa eSolução:
stão Para
o trecho BC temos:
T = 85 N.m = 85000 N.mm
sujeitas aos torques mostrados na figura. Supondo que o módulo de elasticidade N
G = 75 GPa
de cisalhamento seja G = 78 GPa e o eixo tenha diâmetro de 17mm, determinar o = 75000 mm
L =eLm = 250 mm
deslocamento do dente P da engrenagem A. O eixo gira livremente no mancal L = 500 mm
B. d = d = 20 mm
2
AB
CD
BC
ABi
CDi
d ABe = d CDe = 30 mm
d BC = 40 mm
13 
A junta é feita de três chapas de aço A-­‐36 ligadas pelas suas costuras. Determinar L
L
TL T 
!"#$%&'()*+",#)&-%&!(".,&&&/&&&0"#$12"#)#,34(5.67%2#8%9"&
φ =
= 
+
+
o deslocamento da extremidade A em relação à extremidade D quando a junta é GJ G  π(d − d ) πd π(d
32
32

submetida às cargas axiais mostradas. Cada chapa tem espessura de 7 mm. 
AB
AD
c05.qxd
9/19/07
8:18 PM
4
ABe
4
ABi
BC
4
BC
L CD
4
4
CDe − d CDi
32
)





:+,.,6;)2.(&*#,&<(6+".(.,&


250
500
250
+
+

 = 0,0111347 rad = 0,637973 o
75000  π 30 4 − 20 4
π40 4 π 30 4 − 20 4 
32
32
32


Resposta: O ângulo de torção da extremidade A em relação a extremidade D é de 0,638º.
Page85000
207 
φ AD =
(
)
(
)
© 2008 by R.C. Hibbeler. Published by Pearson Prentice Hall, Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material i
copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in writing
14 Comparem os valores da tensão de cisalhamento elástica máxima e do ângulo de torção desenvolvidos em eixos de aço inoxidável 304 com seção transversal circular e quadrada. Cada eixo tem a mesma área de seção transversal de 5200 mm², comprimento de 900 mm e está submetido a um torque de 50 N.m. G = 75GPa. 15 A barra de aço da figura, está submetida a dois conjugados iguais e de sentido contrários, que agem em um plano vertical de simetria. Determinar o valor do momento M que provoca escoamento no material da barra. Adotar: σY=220MPa; a=16mm; b=50mm.