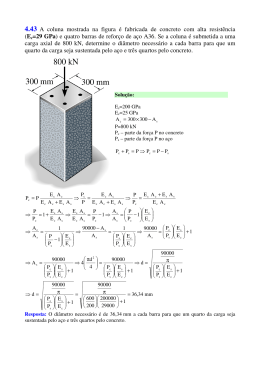
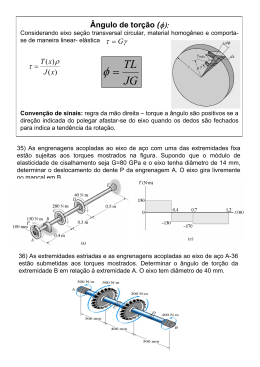
APLICAÇÕES
TEMA: Torção
(1) Um eixo vazado com diâmetro externo de 100 mm e diâmetro interno de 75mm é submetido a um torque de 7.5 kN.m. O
módulo de rigidez G do aço é 80 GPa. Determine:
(a) A máxima tensão de cisalhamento no eixo
(b) A tensão de cisalhamento na altura da superfície interna do eixo
(c) ângulo de torção quando o eixo tem 2m de comprimento
(2) Um eixo sólido de aço, com 14 ft de comprimento, tem diâmetro de 6in. nos primeiros 9 ft e um diâmetro de 4in. nos 5ft
restantes. O eixo está em equilíbrio quando submetido ao três torques mostrados na figura. Considerando para o aço
G=1200 ksi, determine:
(a) A máxima tensão de cisalhamento no eixo
(b) A rotação do ponto B com respeito ao ponto A
(c) A rotação de C com respeito a A
(3) Um motor diesel de um pequeno barco opera a 200 rpm e libera 800 hp para uma caixa de engrenagens com fator de
redução de 4:1 para o eixo propulsor coo mostrado na figura. Ambos os eixos , do motor para a caixa de engrenagens e do
eixo propulsor, são sólidos e feitos de aço. Determine o diâmetro mínimo permissível dos dois eixos, se a máxima tensão
permitida é de 20 ksi e o ângulo de torção em 10ft de comprimento do eixo propulsor não. pode exceder 4º. Despreze as perdas
de potência na caixa de engrenagem e assuma (suposição aproximada) que o eixo propulsor está submetido a torção pura.
Utilize G=12000ksi.
(4) Na tentativa de desapertar um parafuso um trabalhador aplica uma força compressiva P de 111N e um torque de 5.65 N.m
no cabo de uma chave de fenda. O corpo da chave é circular com diâmetro de 12.7 mm . Assumindo que o corpo da chave é
feito de aço inoxidável (Gaço= 77GPa), calcule a máxima tensão de cisalhamento , a
tensão axial σzz e a leitura na roseta de 45ª fixa na superfície do corpo da chave.
(5)Um eixo de aço e um tubo de alumínio, concêntrico ao de aço, são fixos pela base e têm pinos fixos no topo. Um torque é
aplicado através de uma barra rígida que é forçada contra os pinos. O eixo de aço precisa girar 2º antes da barra entrar em
contato com todos os quatro pinos. Calcular o torque necessário para girar a barra rígida de 4º e as tensões em cada eixo neste
momento. Utilize Gaço= 77GPa e Gal= 26GPa
(6) Um sistema de torção como o mostrado na figura consiste em eixo sólido de bronze (CD) e um tubo de alumínio (EF) com
o núcleo em aço. As extremidades C e F são fixas em paredes rígidas e o núcleo de aço do eixo EF está conectado a um
flange em E., de tal forma que o alumínio e o aço atuam com um eixo único. Os dois flanges D e E são aparafusados e a folga
nos parafusos permite que o flange D gire 0.03rad antes que EF receba alguma carga. Determine a máxima tensão de
cisalhamento material dos eixos, quando um torque Mt=54kn.m é aplicado no flange D. (Bronze: G=45GPa, Aço: G=80GPa,
Alumínio G=28GPa).
(7) Um cilindro de paredes delgadas é submetido a um momento torsor T . Qual é a tensão no elemento
plano H da seção transversal E do cilindro, distante das extremidades, se assumirmos que as tensões não
variam ao longo da espessura t. Quais são as tensões no elemento plano G da seção F, distante das
extremidades, inclinada de 45º em relação ao plano xz ?
Adotar: T = 57.5 Nm, t= 5mm e d= 75 mm
y
F
T
E
H
d
z
t
x
x
(7)- Duas partes de um duto cilíndrico cujo diâmetro externo é 200mm e o interno é 198mm, são soldadas
segundo o ângulo θ , como mostra a figura. O duto está sujeito a uma pressão interna de 2 MPa e um torque de
6kNm. A solda deve resistir a uma tensão normal de no máximo 70Mpa. Obtenha o menor valor (positivo)
admissível para θ . Esquematize seu resultado graficamente. (3pontos)
T
θ
x
(8) Um eixo maciço de latão de diâmetro igual a 30 mm é conectado a um tubo de aço carbono de
30 mm
de diâmetro 2.54 mm de espessura. O conjunto está fixado entre duas paredes rígidas quando um torque
concentrado de 500 Nm é aplicado na interface. Sabendo-se que o comprimento total do conjunto é igual a 4m,
pede-se: (4pontos)
(a) Qual deve ser o comprimento do eixo de latão para que o torque transmitido aos dois eixos seja o mesmo?
(b) Determine a tensão máxima no latão e no aço.
(c) A rotação na interface.
Eaço = 200 GPa
νaço = 0.27
Latão
Aço
Elatão = 100 GPa
νlatão= 0.35