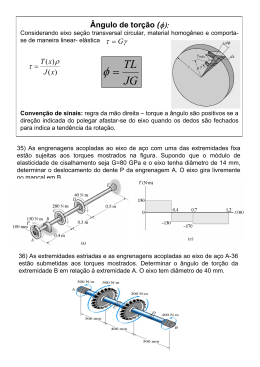
Resistência dos Materiais
Aula 6 – Estudo de Torção,
Transmissão de Potência e Torque
Definição de Torque
Torque é o momento que
tende a torcer a peça em
torno de seu eixo
longitudinal. Seu efeito é de
interesse principal no
projeto de eixos ou eixos de
acionamento usados em
veículos e maquinaria.
Resistência dos Materiais
Deformação por Torção
Resistência dos Materiais
Equação da Torção
Quando um torque externo é aplicado a um eixo, cria um
torque interno correspondente no interior do eixo.
A equação da torção relaciona o torque interno com a
distribuição das tensões de cisalhamento na seção
transversal de um eixo ou tubo circular.
Para material linear-elástico aplica-se a lei de Hooke.
τ = G ⋅γ
onde: G = Módulo de rigidez
γ = Deformação por cisalhamento
Resistência dos Materiais
Equação da Torção
τ máx
T ⋅c
=
J
T ⋅ρ
τ=
J
onde:
τ = Tensão de cisalhamento no eixo
T = Torque interno resultante que atua na
seção transversal
J = Momento de inércia polar da área da seção
transversal
c = Raio externo do eixo
ρ = Raio medido a partir do centro do eixo
Resistência dos Materiais
Dimensionamento de Eixo Sólido
Momento de inércia polar:
c
J = ∫ ρ ⋅ dA
2
J = ∫ ρ 2 ⋅ (2 ⋅ π ⋅ ρ ⋅ dρ )
0
A
c
J = 2 ⋅ π ∫ ρ 3 ⋅ dρ
0
2 ⋅π ⋅ ρ
J=
4
J=
4
c
0
π ⋅ c4
2
Resistência dos Materiais
Falha na Torção
Resistência dos Materiais
Dimensionamento de Eixo Tubular
Momento de inércia polar:
J=
(
π ⋅ ce 4 − ci 4
)
2
Resistência dos Materiais
Exercício 4
1) O tubo mostrado na figura tem um diâmetro interno de 80 mm e diâmetro
externo de 100 mm. Supondo que sua extremidade seja apertada contra o
apoio em A por meio de um torquímetro em B, determinar a tensão de
cisalhamento desenvolvida no material nas paredes interna e externa ao
longo da parte central do tubo quando são aplicadas forças de 80 N ao
torquímetro.
Resistência dos Materiais
Transmissão de Potência
Eixos e tubos com seção
transversal circular são
freqüentemente empregados
para transmitir a potência
gerada por máquinas. Quando
usados para essa finalidade,
são submetidos a torque que
dependem da potência gerada
pela máquina e da velocidade
angular do eixo.
Resistência dos Materiais
Definição de Potência
A potência é definida como o
trabalho realizado por unidade
de tempo:
T ⋅ dθ
P=
dt
Onde:
T = Torque aplicado
dθ = Ângulo de rotação
Sabe-se que a
velocidade angular do
eixo é dada por:
ω=
dθ
dt
Portanto:
P = T ⋅ω
No SI, a potência é expressa em watts
1W = 1Nm/s
Resistência dos Materiais
Relação Potência-Freqüência
No caso da análise de máquinas e
mecanismos, a freqüência de rotação
de um eixo, é geralmente conhecida.
Expressa em hertz (1Hz = 1 ciclo/s),
ela representa o número de revoluções
que o eixo realiza por segundo.
Portanto, a equação da potência pode
ser escrita do seguinte modo:
P = 2 ⋅π ⋅ f ⋅T
Como 1 ciclo = 2π rad,
pode-se escrever que:
ω = 2 ⋅π ⋅ f
Resistência dos Materiais
Dimensionamento de Eixos
Quando a potência transmitida por um
eixo e sua rotação são conhecidas, o
torque no eixo pode ser determinado.
Conhecendo-se o torque atuante no
eixo e a tensão de cisalhamento do
material é possível determinar a
dimensão do eixo a partir da equação
da torção da seguinte forma:
J
T
=
c τ adm
Para eixo maciço:
J=
π ⋅ c4
2
Para eixo tubular:
J=
π ⋅ (ce 4 − ci 4 )
2
Resistência dos Materiais
Exercícios Propostos
1) O eixo maciço de 30 mm de diâmetro é usado para transmitir os torques
aplicados às engrenagens. Determinar a tensão de cisalhamento desenvolvida
nos pontos C e D do eixo.
Resistência dos Materiais
Exercícios Propostos
2) O eixo maciço de alumínio tem diâmetro de 50 mm. Determinar a tensão de
cisalhamento máxima absoluta nele desenvolvida e traçar o gráfico da distribuição
cisalhamento-tensão ao longo de uma reta radial onde o cisalhamento é máximo.
Considerar T1 = 20 Nm.
Resistência dos Materiais
Exercícios Propostos
3) O eixo de aço está submetido à carga de torção mostrada. Determinar a tensão
de cisalhamento desenvolvida nos pontos A e B e desenhar o gráfico da tensão de
cisalhamento nos elementos de volume localizados nesses pontos. O eixo onde A e
B estão localizados tem raio externo de 60 mm.
Resistência dos Materiais
Exercícios Propostos
4) O acoplamento é usado para acoplar dois eixos. Supondo que a tensão de
cisalhamento nos parafusos seja uniforme, determinar o número de parafusos
necessários para que a tensão de cisalhamento máxima no eixo seja igual à tensão
de cisalhamento nos parafusos. Cada parafuso tem diâmetro d.
Resistência dos Materiais
Exercícios Propostos
5) A bomba opera com um motor que tem potência de 85 W. Supondo que o
impulsor em B esteja girando a 150 rpm, determinar a tensão de cisalhamento
máxima desenvolvida em A, localizada no eixo de transmissão que tem 20 mm de
diâmetro.
Resistência dos Materiais
Resistência dos Materiais
Aula 7 – Estudo de Torção,
Ângulo de Torção
Ângulo de Torção
O projeto de um eixo depende de limitações na
quantidade de rotação ou torção ocorrida quando o eixo
é submetido ao torque, desse modo, o ângulo de torção
é importante quando se analisam as reações em eixos
estaticamente indeterminados.
φ=∫
L
0
T ( x) ⋅ dx
J ( x) ⋅ G
φ = Ângulo de torção de uma extremidade do eixo em relação à outra.
T(x) = Torque interno na posição arbitrária x.
J(x) = Momento de inércia polar do eixo expresso em função de x.
G = Módulo de elasticidade ao cisalhamento do material.
Resistência dos Materiais
Cálculo para Área e Torque Constantes
Normalmente, o material é homogêneo, de modo que G é constante, bem
como, a área da seção transversal e o torque aplicado também são
constantes, portanto, a equação que determina o ângulo de torção pode ser
expressa do seguinte modo:
T ⋅L
φ=
J ⋅G
Se o eixo estiver sujeito a diversos torques diferentes, ou a área da seção
transversal e o módulo de elasticidade mudarem abruptamente de uma região
para outra, o ângulo de torção pode ser determinado a partir da adição dos
ângulos de torção para cada segmento do eixo, assim:
T ⋅L
φ =∑
J ⋅G
Resistência dos Materiais
Convenção de Sinais
A direção e o sentido do torque aplicado é definido a partir da aplicação
da regra da mão direita. Torque e ângulo serão positivos se a direção
indicada pelo polegar for no sentido de afastar-se do eixo.
Resistência dos Materiais
EIXO SUJEITO A DIVERSOS TORQUES
(DIAGRAMA REPRESENTATIVO)
Resistência dos Materiais
Exercício 1
1) As engrenagens acopladas ao eixo de aço com uma das extremidades
fixa estão sujeitas aos torques mostrados na figura. Supondo que o módulo
de elasticidade de cisalhamento seja G = 80 GPa e o eixo tenha diâmetro de
14 mm, determinar o deslocamento do dente P da engrenagem A. O eixo
gira livremente no mancal em B.
Resistência dos Materiais
Exercícios Propostos
1) Os dois eixos de aço maciço mostrados na figura estão acoplados por meio de
engrenagens. Determinar o ângulo de torção da extremidade A do eixo AB
quando é aplicado o torque T = 45 Nm. Supor G = 80 GPa. O eixo AB é livre para
girar nos mancais E e F, enquanto o eixo DC é fixo em D. Cada eixo tem
diâmetro de 20 mm.
Resistência dos Materiais
Exercícios Propostos
3) O eixo de aço A-36 está composto pelos tubos AB e CD e por uma parte maciça
BC. Apóia-se em mancais lisos que lhe permitem girar livremente. Se as
extremidades estão sujeitas a torques de 85 Nm, qual o ângulo de torção da
extremidade A em relação à extremidade D? Os tubos tem diâmetro externo de 30
mm e diâmetro interno de 20 mm. A parte maciça tem diâmetro de 40 mm.
Resistência dos Materiais
Exercícios Propostos
4) O eixo maciço de aço A-36 tem 3 m de comprimento e diâmetro externo de 50
mm. Requer-se que transmita 35 kW de potência do motor E para o Gerador G.
Determinar a menor velocidade angular que o eixo pode ter se a máxima torção
admissível é de 1°.
Resistência dos Materiais