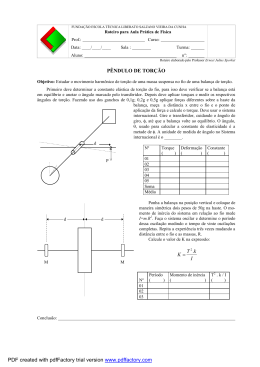
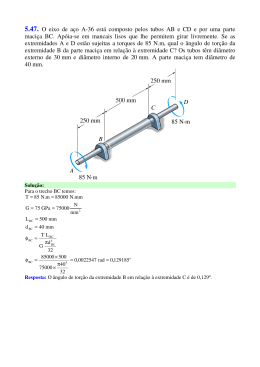
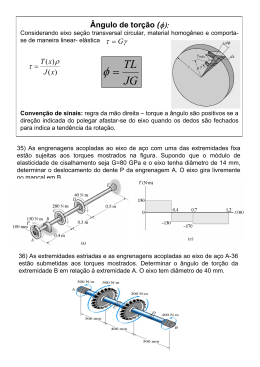
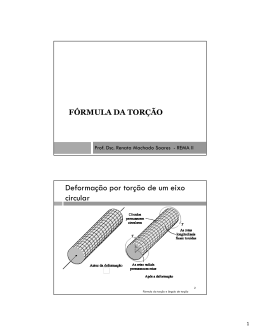
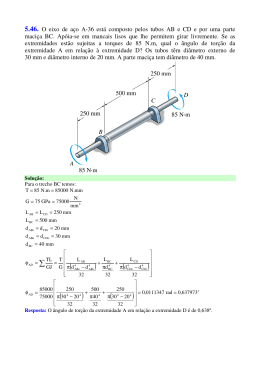
5.43. Um eixo está submetido a um torque T. Comparar a eficácia do tubo mostrado
na figura com a de um eixo de seção maciça de raio c. Para isso, calcular a
porcentagem de aumento na tensão de torção e no ângulo de torção por unidade de
comprimento do tubo em relação aos valores do eixo de seção maciça.
Solução:
As tensões de torção são:
Tc
Tc
Tc
t
τ max
=
=
=
Jt
 πc 4 π(c / 2) 4   πc 4 15 

 
−
× 
2
 2
  2 16 
Tc
Tc
τ mmax =
=
Jt
 πc 4 


 2 
Os ângulos de torção são:
TL
TL
t
φ max
=
=
GJ t
 πc 4 π(c / 2) 4
G 
−
2
 2
τ mmax =
Tc
e tensão
 πc 4 15 

× 
2 16  16

=
=
= 1,0667
Tc
15
 πc 4 


 2 
TL
=
GJ t
TL
 πc 4
G 
 2



=
TL
 πc 4 15 
G 
× 
 2 16 



TL
e ângulo
 πc 4 15 
G 
× 
2 16  16

=
=
= 1,0667
TL
15
 πc 4 

G 
 2 
Resposta: As eficiências de tensão de torção e ângulo de torção são iguais e valem um aumento de
6,67% do eixo vazado em relação ao eixo maciço.