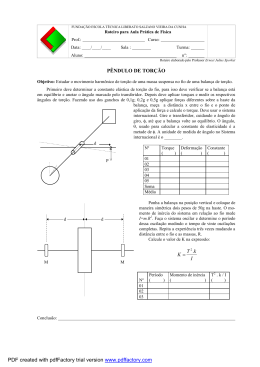
Aula 15 -­‐ Estudo de Torção e Ângulo de Torção. Prof. Wanderson S. Paris, M.Eng. [email protected] Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Ângulo de Torção O projeto de um eixo depende de limitações na quan5dade de rotação ou torção ocorrida quando o eixo é subme5do ao torque, desse modo, o ângulo de torção é importante quando se analisam as reações em eixos esta5camente indeterminados. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Ângulo de Torção φ = Ângulo de torção de uma extremidade do eixo em relação à outra. T(x) = Torque interno na posição arbitrária x. J(x) = Momento de inércia polar do eixo expresso em f(x). G = Módulo de elas5cidade ao cisalhamento do material. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Cálculo para Área e Torque Constantes Normalmente, o material é homogêneo, de modo que G é constante, bem como, a área da seção transversal e o torque aplicado também são constantes, portanto, a equação que determina o ângulo de torção pode ser expressa do seguinte modo: Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Cálculo para Área e Torque Constantes Se o eixo es5ver sujeito a diversos torques diferentes, ou a área da seção transversal e o módulo de elas5cidade mudarem abruptamente de uma região para outra, o ângulo de torção pode ser determinado a par5r da adição dos ângulos de torção para cada segmento do eixo, assim: Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Convenção de Sinais A direção e o sen5do do torque aplicado é definido a par5r da aplicação da regra da mão direita. Torque e ângulo serão posi5vos se a direção indicada pelo polegar for no sen5do de afastar-­‐se do eixo. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS EIXO SUJEITO A DIVERSOS TORQUES Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Exercício 1 1) As engrenagens acopladas ao eixo de aço com uma das extremidades fixa estão sujeitas aos torques mostrados na figura. Supondo que o módulo de elas5cidade de cisalhamento seja G = 80 GPa e o eixo tenha diâmetro de 14 mm, determinar o deslocamento do dente P da engrenagem A. O eixo gira livremente no mancal em B. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Solução do Exercício 1 Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Solução do Exercício 1 Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS qxd
9/19/07
8:16 PM
Page 186
Exercício 2 © 2008 by R.C. Hibbeler. Published by Pearson Prentice Hall, Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This ma
copyright laws as they currently exist. No portion of this material may be reproduced, in any form or by any means, without permission in w
O Parafuso de aço A-­‐36 com 8 mm de diâmetro está parafusado firmemente ao bloco em A. Determine as forças conjugadas F que devem ser aplicadas à chave de torque de modo que a tensão de cisalhamento máxima no parafuso seja de 18 Mpa. Calcule também o deslocamento correspondente de cada força F necessários para causar essa tensão. Considere que a chave de torque seja rígida. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Solução do Exercício 2 Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Solução do Exercício 2 Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS T
Exercícios Propostos c
2
100 ft
T
c
Pr
c
5–51. The engine of the
to the rotor shaft AB w
1200 rev>min. Determine
of the shaft AB if the allow
and the vibrations limit th
0.05 rad. The shaft is 2 ft lo
Prob. 5–48
[P68] O eixo de aço A-­‐36 é composto pelos tubos AB e CD e uma seção maciça BC. Está apoiado em m•ancais lisos ue permitem ue 5–49. The A-36
steelq
axle
is made
from tubes ABq
and
CDele gire and a solid section BC. It is supported on smooth bearings
livremente. Se as engrenagens, pallow
resas às efreely.
xtremidades dends,
os are
eixos, that
it to rotate
If the gears, fixed to its
*5–52. The engine of the
subjected to 85-N # m torques, determine the angle of twist
to the rotor shaft AB w
forem subme5das a torques de 5 ANrelative
m, determine o âhave
ngulo de torção of 8
gear
to gear D. The tubes
an outer
1200 rev>min. Determine t
diameter of 30 mm and an inner diameter of 20 mm. The
the shaft AB if the allowab
da engrenagem A em relação àsolid
engrenagem s tubos têm diâmetro section has a diameterD
of. 40O
mm.
and the vibrations limit th
rad. The shaft is 2 ft lo
externo de 30 mm e diâmetro interno de 20 mm. A seção maciça 0.05
tem diâmetro de 40 mm. 400 mm
D
85 N!m
250 mm
C
400 mm
B
A
A
85 N!m
Prob. 5–49
Prof. Wanderson S. Paris -­‐ [email protected] Prob
MECÂNICA DOS SÓLIDOS Exercícios Propostos PTER
5
TORSION
[P69] As extremidades estriadas e as engrenagens acopladas ao eixo 9*5–56.
splined
ends and gears attached
the A-36 mostrados. m-diameter A-36
steel
shaft
is-­‐36 subjected
de a
ço A
7
5x10
Pa eThe
stão subme5das aos ttoorques steel shaft are subjected to the torques shown. Determine
wn. Determine the angle of twist of the
the angle
twist of end
respect to end A. The
Determinar o ângulo de oftorção dBa with
extremidade B shaft
em relação à has a diameter of 40 mm.
extremidade A. O eixo tem diâmetro de 40 mm. 300 N!m
500 N!m
A
200 N!m
A
D
20 N!m
C
30 N!m
600 mm
200 mm
400 N!m
300 mm
D
B
400 mm
800 mm
m
500 mm
Prob. 5–53
Prof. Wanderson S. Paris -­‐ [email protected] •5–57.
Prob. 5–56
The motor delivers 40 hp to the 304 stainless steel
MECÂNICA DOS SÓLIDOS Exercícios Propostos [P70] A turbina desenvolve 150 kW de potência, que é transmi5da às engrenagens de tal modo que C e D recebem quan5dades iguais. Se a rotação do eixo de aço A-­‐36 de 100 mm de diâmetro for igual a 150 rev/min, determine a tensão de cisalhamento máxima absoluta no eixo e a rotação da extremidade B em relação a E. O mancal em C permite que o eixo gire livremente. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS 5
600 mm
B
0.6
75 mm
900 mm
Exercícios Propostos T1
Probs. 5–6
C
Probs. 5–66/67
5–71. Consider the general pr
made from m segments, each havi
modulus Gm . If there are n torqu
write a computer program that
the angle of twist of its end A. S
program using the values L
G1 = 30 GPa, L2 = 1.5 m, c2
T1 = - 450 N # m, d1 = 0.25 m, T
*5–68.
shafts
arefeitos made ofdL2
[P71] Os eixos de 30 mThe
m 30-mm-diameter
de diâmetro são e tool
aço ferramenta steel and are supported on journal bearings that allow the
L2 e estão apoiados em mfreely.
ancais ue patermitem os eofixos girarem shaft to
rotate
If theqmotor
A develops aatorque
T = 45 N # m on the shaft AB, while the turbine at E is fixed
livremente. Se o from
motor em A desenvolver um torque T = 45 Nm no turning, determine the amount of rotation of gears B
and a
C. turbina em E é fixa e não pode girar, determine eixo AB, enquanto a quan5dade de rotação das engrenagens B e C. A
45 N!m
Tn
T2
B
1.5 m
0.5 m
50 mm
D
T1
C
E
75 mm
0.75 m
A
d1
d2
L1
Prof. Wanderson S. Paris -­‐ [email protected] Prob. 5–68
MECÂNICA DOS SÓLIDOS Prob. 5–7
Exercícios Propostos [P72] O conjunto é feito de aço A-­‐36 e é composto por uma haste maciça de 15 mm de diâmetro conectada ao interior de um tubo por meio de um disco rígido em B. Determine o ângulo de torção em A. O tubo tem diâmetro externo de 30 mm e espessura de parede de 3 mm. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS Referências Bibliográficas •  hJp://www.cronosquality.com/aulas/ms/index.html •  Hibbeler, R. C. -­‐ Resistência dos Materiais, 7.ed. São Paulo :Pearson Pren5ce Hall, 2010. •  BEER, F.P. e JOHNSTON, JR., E.R. Resistência dos Materiais, 3.o Ed., Makron Books, 1995. •  Rodrigues, L. E. M. J. Resistência dos Materiais, Ins5tuto Federal de Educação, Ciência e Tecnologia – São Paulo: 2009. •  BUFFONI, S.S.O. Resistência dos Materiais, Universidade Federal Fluminense – Rio de Janeiro: 2008. Prof. Wanderson S. Paris -­‐ [email protected] MECÂNICA DOS SÓLIDOS