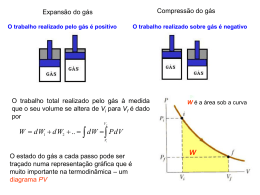
CALOR, TRABALHO E A 1ª. LEI
DA TERMODINÂMICA
Anotações baseadas no texto “Fundamentos
da Termodinâmica de Sontagg, R. E. ,
Borgnakke, C. e Van Wylen, G. J.
CALOR, TRABALHO E A 1ª. LEI DA TERMODINÂMICA
Trabalho e calor são a essência da termodinâmica. Assim é fundamental o
entendimento das duas definições tendo em vista que a análise correta
de muitos problemas térmicos depende da distinção entre elas.
Trabalho de um sistema
Definição. Um sistema realiza trabalho se o único efeito sobre o meio
(externo ao sistema) PUDER SER o levantamento de um peso.
Trabalho atravessa a fronteira do sistema neste caso?
Caso 1.
Trabalho atravessa a fronteira do sistema nesse caso?
Caso 1.
Trabalho Mecânico.
dW  F x dx  F .dx . cos   F .dx
2
W 
 F .dx
1
Se F constante ,
mov. retilíneo
l2
2
W 
 F .d l
1

 F .dl
l1
l2
 W  F  dl  Fl
l1
dW  F .d s
W 
 dW

 F .d s
O trabalho de um sistema é considerado positivo quando é recebido pelo
sistema e o trabalho realizado é negativo quando sai do sistema. O símbolo W
designa o trabalho termodinâmico.
Unidades de Trabalho
1 J = 1N.m
Potência e unidades de potência.
W
W 
t
Watt 
J
s
Trabalho Realizado devido ao Movimento de Fronteira
de um Sistema Compressível Simples num Processo
Quase-Estático.
Vamos tirar um dos pequenos pesos do êmbolo provocando um movimento para cima
deste, de uma distância dx. Podemos considerar este pequeno deslocamento de um
processo quase-estático e calcular o trabalho, dW, realizado pelo sistema durante
este processo.
A força total sobre o êmbolo é P. A, onde P é a pressão do gás e A é a área do êmbolo.
Portanto o trabalho W é:
a) na compressão W > 0
 
dW   p . A .n .d x   p . A .dx . cos 180   p .dV  W 
V2
 pdV
<0
V1
b)
na expansão W < 0
 
dW   p . A .n .d x   p . A .dx . cos 0    p .dV  W  
V2
 pdV
V1
>0
Correção da fórmula:
V2
dW  
 pdV
Eq. 3.6.
V1
Esse trabalho é o realizado devido ao movimento de fronteira de um sistema
compressível simples num processo quase-estático.
O trabalho realizado devido ao movimento de fronteira, durante um dado
processo quase-estático, pode ser determinado pela integração da Eq. 3.6.
Entretanto essa integração somente pode ser efetuada se conhecermos a
relação entre P e V durante esse processo. Essa relação pode ser expressa na
forma de uma equação ou pode ser mostrada na forma gráfica .
Visualização do trabalho num processo quase-estático.
W12 > 0
W21 < 0
No inicio do processo o êmbolo está na posição 1 e a pressão é relativamente baixa. Esse estado está
representado no diagrama P x V como mostra a Figura5. No fim do processo, o êmbolo está na posição
2 e o estado correspondente do sistema é mostrado pelo ponto 2 no diagrama P x V. Se a compressão
é um processo quase-estático e, durante o processo, o sistema passa através dos estados indicados
pela linha que liga os pontos 1 e 2 do diagrama P x V. O trabalho realizado sobre o gás durante este
processo de compressão pode ser determinado pela integração da Eq. 3.6, resultando:
V2
W 12    pdV
V1
Trabalho num processo quase-estático.
Uma nova consideração do diagrama P x V, conduz a uma outra
conclusão importante. É possível ir do estado 1 ao estado 2 por
caminhos quase-estáticos muito diferentes, tais como A, B ou C.
Como a área sob a curva representa o trabalho para cada processo é
evidente que o trabalho envolvido em cada caso é uma função não
somente dos estados iniciais e finais do processo, mas também, do
caminho que se percorre ao ir de um estado a outro.
Por esta razão, o trabalho é chamado de função de linha, ou em
linguagem matemática, W é uma diferencial inexata, diferente das
diferencias exatas que dependem apenas do estado inicial e final
,como veremos é o caso da energia cuja diferencia é indicada como dE.
Trabalho processos quase-estáticos de transformação.
1-A relação entre P e V pode ser dada em termos de dados experimentais ou
na forma gráfica. Neste caso podemos determinar a integral da Eq. 3.7 por
integração gráfica ou numérica.
2-A relação entre P e V é tal que seja possível ajustar uma relação
analítica entre as variáveis e, assim, é possível fazer diretamente a
integração da expressão.
Processo quase-estático a pressão constante (isobárico).
p  cte  p 1  p 2
V2
V1
V1
V2
W    pdV    pdV   p V 2  V 1 
Trabalho processos quase-estáticos de transformação.
Processo a temperatura constante (isotérmico)
pV  cte  p 1V 1  p 2 V 2
V2
V1
W    pdV   
V1
V2
cte
V
dV   P1V 1 ln V 2 / V 1 
Processo politrópico
pV
n
n
 cte  p1V1  p 2V 2
p 
cte
V
n
n
Processo politrópico
V2
V1
W    pdV   cte
V1
W 
W 
dV
V
n
V2
cte
n1
V
1 n
2
1


  cte 
V
 n 1
1 n
 V1
 n 1
V2
V1

p 2 V 2  p 1V 1

n
n 
1 n
1 n
p
V
V

p
V
V

 2 2

2
1 1
1
n1
n1

1
Note-se que este resultado é válido para qualquer valor do expoente n, exceto n = 1.
Para n = 1, tem-se;
pV  cte  p1V1  p 2V 2
V2
W    pdV   cte
V1
V1
dV
V
V2
V
  P 1V 1 * ln  2
 V1

V
   P 2 V 2 * ln  2

V

 1




Exemplo 3.1. Considere como sistema o gás contido no cilindro mostrado na
figura 8, provido de um êmbolo sobre o qual são colocados vários pesos
pequenos. A pressão inicial é de 200 kPa e o volume inicial do gás é de 0,04 m3.
a) Calcular o trabalho realizado pelo sistema durante esse processo
se for colocado um bico de Bunsen embaixo do cilindro e deixa-se
que o volume do gás aumente para 0,1 m3 , enquanto a pressão
permanece constante.
V2
P cte
W 12   p  dV   p  V   p V 2  V 1   - 200000 * (0,1 - 0,04)  - 12,0 kJ
V1
b) Considerando o mesmo sistema e as mesmas condições iniciais e
finais, porém, ao mesmo tempo em que o bico de Bunsen está sob
o cilindro e o êmbolo se levanta, removamos os pesos deste, de tal
maneira que durante o processo a temperatura se mantém
constante.
Se como gás ideal: PV = mRgT
V
W   P 1V 1 * ln  2
 V1

 0 ,1 
   200000 * 0 , 04 * ln 
   7,33 kJ

 0 , 04 

c) Consideremos o mesmo sistema porém, durante a troca de calor removamos os
pesos de tal maneira que a expressão, PV1,3 = constante, descreva a relação entre a
pressão e o volume durante o processo. Novamente o volume final é 0,1 m3. Calcular o
trabalho envolvido.
1, 3
p 1V 1
 p 2V 2
1, 3

 0 , 04 
P2= 200000 *  0 ,10 


W 
p 2V 2  p 1V 1
n 1

200000 * 0 , 04
1, 3
 p 2 0 ,1
1, 3
1,3
= 60,77 kPa
60773 * 0 ,1  200000 * 0 , 04
0,3
  6,41 kJ
d) Consideremos o sistema e o estado inicial dado nos três primeiros exemplos,
porém mantenhamos o êmbolo preso por meio de um pino, de modo que o volume
permaneça constante. Além disso, façamos com que o calor seja transferido do
sistema para o meio até que a pressão caia a 100 kPa. Calcular o trabalho.
Como dW = P.dV, para um processo quase-estático, o trabalho é igual a zero
porque, neste caso, não há variação do volume, isto é, dV=0.
Exemplo 3.2. Um cilindro com êmbolo móvel, como mostrado na figura, contém 3
kg d’água no estado de vapor úmido com título igual a 15 % e pressão de 2,0 bar
(estado 1 ). Esse sistema é aquecido à pressão constante até se obter o título igual
a 85 % (estado 2 ). Pede-se: a) Representar o processo em um diagrama P-V. b)
Calcular o trabalho realizado pelo vapor durante o processo.
Tsat= 120,2 oC
b) O trabalho devido ao movimento de fronteira é:
W 12   p .m .v 2  v 1 
Da tabela de propriedades de saturação, para o estado 1, P = 200kPa obtemos vl
= 0,001061 m3 /kg, vv= 0,8857 m3 /kg.
v1 = vl + y ( vv-vl) = 0,001061 + 0,15 ( 0,8857 -0,001061) = 0,13376 m3 /kg.
quando y =0,85
v1 = vl + y ( vv-vl) = 0,001061 + 0,85 ( 0,8857 -0,001061) = 0,7530 m3 /kg
Substituindo na expressão do trabalho, Eq.3.07 tem-se:
W12 = - 2,0.105 x 3 x (0,7530 -0,133756 ) J
W12 = - 3,715.105 [ J ] ou W12 =- 371,5 kJ
Exemplo 3.3 Um cilindro com êmbolo móvel, como mostrado na figura, contém 5
kg d’água no estado de vapor úmido com título igual a 20 % e pressão de 5,0 bar
(estado 1). Esse sistema é aquecido à pressão constante até se obter a
temperatura de 200 OC (estado 2). Pede-se: a) Representar o processo em um
diagrama P-v; b) Determinar o trabalho realizado pela substância de trabalho
contra o êmbolo, em kJ
a)
b) O trabalho devido ao movimento de fronteira é:
Da tabela de propriedades de saturação, para o estado 1, P = 500 kPa obtem-se:
vl1 = 0,001093 m3 /kg, vv1= 0,3749 m3 /kg.
v1 = vl1 + x ( vv1-vl1) = 0,001093 + 0,2 ( 0,3749 -0,001093) = 0,0759 m3 /kg.
Da tabela de vapor superaquecido para P2 = 500 kPa e T2 = 200 oC, obtem-se:
v2 = 0,42492 m3 / kg. Assim o trabalho entre o estado 1 e 2 resulta em:
W 12   p .m .v 2  v 1 
W 12   5 . 10 * 5 * .0 , 42492  0 , 0759
5

= -872,7kJ.
Trabalho contra uma mola
Exemplo 3.4. Considere o sistema mostrado na Figura . O volume inicial do ar no
interior do conjunto êmbolo-cilindro é de 0,03 m3, neste estado a pressão interna
é de 1,1 kgf/cm2, suficiente para contrabalançar a pressão atmosférica externa e
o peso do êmbolo. A mola toca o êmbolo mas não exerce qualquer força sobre o
mesmo nesse estado. O sistema (ar) é então aquecido até que o volume do sistema
seja o dobro do volume inicial. A pressão final do sistema é de 3,5 kgf/cm2 e,
durante o processo a força de mola é proporcional ao deslocamento do êmbolo a
partir da posição inicial [ F = k(x-xo)]. Pede-se:
a) Considerando o ar como sistema, calcular o trabalho realizado pelo sistema
b) Mostrar o processo em um diagrama, P - v
Obs. 1 kgf/cm2 = 9,806 N *104 cm2/m2 = 98,06 kPa= 0,09806 MPa
2
a) sendo o trabalho W12 =


pdV
, e, sendo P = ( Patm + Pêmb + Pmola ), temos:
1
2
W     Patm  Pemb  Pmola dV  
1
k x  xo  
mg

P



 dV
  atm A
A

1
2
kA  x  x o  
k V  V o  
mg
mg


W     Patm 


 dV     Patm 
 dV
2
A
AA
A
A


1 
1 
2
2
kV o kV 
 ' k V  V o  

W    P 
dV


p

 2 dV


2
2

A
A
A 

1 
V1 
V2
2
V2
kV 

 p  p2 
 p1  p 2 
W     p  2 dV    1
V  
 V 2  V 1 
A 
2
2




V1 
W 12  
1
2
 p1 
p 2 V 2  V 1   
1
2
1,1  3 , 5 0 , 09806
. 10
6
0 , 6  0 , 3    6 , 77 kJ
Outras Formas de Realização de Trabalho.
Trabalho de um eixo

 
T  F  r  F .r .sen 90   F .r
n=> no de revoluções
T
 F
r
tf
w

F .ds  F .  ds  2 . .r .n . F
0
w
T
. 2  .r .n  2  .n .T
r
w  F . s  F .v  2  .n .T
Potencia de um eixo
Exercício 3.5. Qual a potencia transmitida por um eixo de um automóvel
quando o troque aplicado é 200 N .m e a sua rotação é 4000 rpm
Sinal?
Motor < 0
Turbina < 0
Bomba
hidráulica > 0
Calor
Calor é definido como sendo a forma de energia transferida através da fronteira
de um sistema a uma dada temperatura, a um outro sistema (ou meio ) numa
temperatura inferior, em virtude da diferença de temperatura entre os dois
sistemas. Isto é, o calor é transferido do sistema de maior temperatura ao sistema
de temperatura menor e a transferência de calor ocorre unicamente devido à
diferença de temperatura entre os dois sistemas.
Um outro aspecto dessa definição de calor é que um corpo ou sistema nunca contém
calor.
Calor só pode ser identificado quando atravessa a fronteira. Assim o calor é um
fenômeno transitório.
Comparação entre Calor e Trabalho
Há muita semelhança entre calor e trabalho, que passaremos a
resumir:
a) O calor e o trabalho são, ambos, fenômenos "transitórios". Os
sistemas nunca possuem calor ou trabalho, porém qualquer um deles
ou, ambos, atravessam a fronteira do sistema, quando o sistema
sofre uma mudança de estado.
b) Tanto o calor como o trabalho são fenômenos de fronteira. Ambos
são observados somente nas fronteiras do sistema, e ambos
representam energia atravessando a fronteira do sistema.
c) Tanto o calor como o trabalho são funções de linha e têm
diferenciais inexatas.
Convenção de sinais
Calor e trabalho
O que atravessa a fronteira?
a)
b)
3.6. Um condensador de grande porte (trocador de calor ) utilizado numa grande central de
potencia deve transferir 100 MW da água que escoa num ciclo de potencia para a água de
refrigeração (bombeada de um reservatório). Considerar que a parede dos tubos do trocador de
calor que separa a água aquecida d’água de refrigeração tenha uma espessura de 4 mm e seja feita
de aço cuja condutibilidade térmica nas condições de utilização seja 50 W/m.K. O projeto do
trocador considera que a diferença de temperatura máxima entre os dois fluidos seja 5 oC.
Admitindo que os coeficientes de transferência de calor (convectivos) sejam muito grandes
determinar a área mínima de transferência do condensador
3.7. A área total de troca de calor de um condensador de uma geladeira domestica é 1 m2. O
temperatura da superfície externa do condensador é 35 oC e o coeficiente médio de
transferência de calor (convectivo) é 15 w/m2. K. Qual a quantidade de calor transferida para o
ambiente durante 15 minutos de operação da geladeira.Considere a temperatura do ar igual a 20
oC.
Primeira Lei da Termodinâmica
A primeira lei da termodinâmica é comumente chamada de "lei da
conservação da energia". Nos cursos elementares de física, o estudo da
conservação de energia dá ênfase às transformações de energia cinética e
potencial e suas relações com o trabalho.
Uma forma mais geral de conservação de energia inclui os efeitos de
transferência de calor e a variação de energia interna.
Primeira Lei
A energia não pode ser criada ou destruída . Só se pode mudá-la de uma
forma para outra, ou só acrescentá-la a um sistema retirando de outro lugar
(da vizinhança).
Formas de Energia
Energia Cinética. Energia que um objeto possui ao se movimentar com determinada
velocidade ( macroscópica e dependentes de um referencial externo).
Ek  m
V
2
ou
2
ek 
V
2
Unidades?
2
Energia Potencial. Energia que um objeto possui em função de sua altura quando está
submetido a um campo gravitacional( macroscópica).
E p  mgh ou e p  gh
Unidades?
Energia Interna. Energia relacionada à estrutura molecular e sua atividade
molecular e não dependem de referencial externo( microscópica).
U
ou
u
Unidades?
Energia Cinética.
dv ds
E k  W   F .ds   m .a .ds   m
.
ds 
dt ds
W 
 F .ds
 m
Ek  m
 ek 
dv
ds
V
v .ds  m  v .dv 
2
2
2
1
 v 22 v 12 

 m 


2
2


ou
 V 22  V 12
E k  m 
2

ou
 V 22  V 12
e k  
2

2
2
V
m .v
2
2
dv ds
 m ds . dt ds








Energia Potencial.
E p  W 

F .ds 

mg .ds  mg s
h2
h1
 mg  h 2  h1 
 E p  mg  h ou e p  g  h
Energia Interna.
energia sensível
Energia Interna.
energia latente: arranjos molecular (sólido, líquido ou gasoso)
Energias estáticas : armazenadas no sistema.
Energias dinâmicas (interações de energia): identificadas na
fronteira no sistema e representam a energia ganha ou perdida pelo
sistema. O calor e o trabalho.
Energias organizada :energia cinética macroscópica, energia
potencial armazenadas no sistema, trabalho.
Energias aleatória ou desorganizada organizada :energia
cinética microscópica, calor.
Energia de um sistema
E  Ek  E p  U
E m
v
e  ek  e p  u
2
 m . g .h  U
2
e
v
2
 g .h  u
2
Trabalho e calor
Calor e trabalho são fenômenos de fronteira. Ambos são observados
somente nas fronteiras do sistema, e ambos representam energia
atravessando a fronteira do sistema.
Primeira Lei da Termodinâmica para um ciclo
A primeira lei da termodinâmica estabelece que, durante um processo cíclico
qualquer, percorrido por um sistema, a integral cíclica (somatório sobre todo o
ciclo), do calor é proporcional à integral cíclica do trabalho, matematicamente


ciclo
Q  
ciclo
W
Q    W
Toda a experiência efetuada até agora provou a veracidade direta ou indiretamente da
primeira lei. A primeira lei nunca foi contestada e tem sido satisfeita por muitas
experiências físicas diferentes.
Primeira Lei para Mudança de Estado de um
Sistema
Considere-se um sistema que percorre um ciclo, mudando do estado 1 ao estado
2 pelo processo A e voltando do estado 2 ao estado 1 pelo processo B. Este ciclo
está mostrado na Figura. Da primeira lei da termodinâmica temos;

Q    W
2

1
1
Q A 

2
2
Q B    W A 
1
1

2
W B
Primeira Lei para Mudança de Estado de um
Sistema
Agora, consideremos outro ciclo, com o sistema mudando do estado 1 ao estado 2
pelo mesmo processo A e voltando ao estado 1 pelo processo C como indicado na
Figura. Para este ciclo podemos escrever:
2

1

Q A 
12

2
1
Q B    W A 

W B
2
1
21
1 2

Q C    W A 
Q A 
1
2
1

W C
2
Subtraindo a segunda destas equações da primeira, temos,
1

1
Q B 
2

1
1
Q C    W B 
2
2

W C
2
ou reorganizando os termos:
1
1

Q B 
2

1
W B 

2
1
  Q
2
B
1
 W B  
Q C 
2

W C
2
1
  Q
2
C
 W C

Primeira Lei para Mudança de Estado de um
Sistema
Visto que B e C representam caminhos arbitrários entre os estados 1 e 2
concluímos que a quantidade ( Q +  W) é a mesma para qualquer processo entre o
estado 1 e o estado 2.
Em conseqüência, ( Q +  W) depende somente dos estados inicial e final não
dependendo do caminho percorrido entre os dois estados
a quantidade, ( Q +  W ), é uma função de ponto, e portanto, é a diferencial
exata de uma propriedade do sistema. Essa propriedade é a energia total do
sistema e é representada pelo símbolo E. Assim podemos escrever
Q+W=dE
2
E 2  E1 
2
 dE    Q   W   Q
1
1
 E  Q 12  W 12
12
 W 12
Sistema isolado
 E  Q 12  W 12
 E   Ek   Ep   U  0
E  0
U  0
Sistema fechado a V cte.
 E  Q 12  W 12
 E   E k   E p   U  Q 12
Sistema fechado a p cte.
 E  Q 12
 U  Q 12
 E  Q 12  W 12  Q 12  p V 2  V 1 
 E   E k   E p   U  Q 12
 U  Q 12  p V 2  V 1 
U 2  pV 2  U 1  pV 1    H  Q 12
Exemplo 3.8 Um sistema inicialmente em repouso sofre um processo no qual recebe
uma quantidade de trabalho igual a 200 kJ. Durante o processo o sistema transfere
para o meio ambiente uma quantidade de calor igual a 30 kJ. Ao final do processo o
sistema tem velocidade de 60 m/s e uma elevação de 50 m. A massa do sistema é de
25 kg, e a aceleração gravitacional local é de 9,78 m/s2. Determine a variação de
energia interna do sistema durante o processo, em kJ .
Sistema: O sistema sob análise é um sistema fechado, constituído
da massa de 25 kg 2. No estado final o sistema está em equilíbrio
(velocidade uniforme).
1ª Lei: ΔE = Q12 + W12 ou Δ U +Δ EC +Δ EP = Q12 + W12
 EC 
1
2


m v 2  v1 
2
2
1

25 * 60
2
2
0
2
  45000
J
 EP  mg  h 2  h 1   25 * 9 , 78 * 50  0   12225 J
 U    EC   EP  Q  W   30 kJ  45 , 0 kJ  12 , 225 kJ  200 kJ  112 , 775 kJ
Entradas
200 kJ (trabalho)
200 kJ
Variações Internas
45,000 kJ (energia cinética)
12,225 kJ (energia potencial)
112,775 kJ (energia interna
170,000 kJ (variação total)
Saídas
30 kJ (calor)
30 kJ
Exemplo 3.8. Considere 5 kg de vapor de água contida no interior do conjunto
cilindro pistão. O vapor sofre uma expansão do estado 1 onde P = 5,0 bar e T=240
oC para o estado 2 onde P=1,5 bar e T=200 oC. Durante o processo 80 kJ de calor
são transferidos para o vapor. Uma hélice é colocada no interior do conjunto
através de um eixo para homogeneizar o vapor, a qual transfere 18,5 kJ para o
sistema. O conjunto cilindro pistão está em repouso. Determinar a quantidade de
trabalho transferido para o pistão durante o processo de expansão.
caracterização:
1-o vapor é o sistema termodinâmico fechado.
2-não há variação de energia cinética e potencial
1ª Lei: ΔE = Q12 + W12 ou Δ U +Δ EC +Δ EP = Q12 + W12
W12 = Whélice + Wpistão
Wpistao = m(u2 -u1) – Q12 –WHélice
500 kPa
T
200
240
250
u1 = 2707,6 kJ
u
2654,4
u1
2731,2
200 oC
T
100
150
200
u
2658,0
u2
2654,4
u2= 2656,2 kJ
Substituindo os valores numéricos na expressão (2) tem-se:
Wpistao = 5*(2656 2 -2707 6 )kJ . - 80 kJ-18,5 kJ = 257,0 – 80,0 – 18,5 = -365,5 kJ