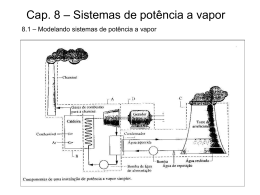
1 Lei na Forma de Taxas e sua
aplicação a Sistemas Abertos
Primeira lei da termodinâmica
em termos de taxa
Muitas vezes é vantajoso usar a primeira lei em termos de taxa, expressando
a taxa média ou instantânea de energia que cruza a fronteira do sistema
como calor e trabalho — e a taxa de variação de energia do sistema.
Procedendo desse modo estamos nos afastando do ponto de vista
estritamente clássico, pois basicamente a termodinâmica clássica cuida de
sistemas que estão em equilíbrio e o tempo não é um parâmetro importante
para sistemas que estão em equilíbrio.
Consideremos um intervalo de tempo dt, durante o qual uma quantidade de calor
dQ atravessa a fronteira do sistema, um trabalho dW é realizado pelo sistema,
a variação de energia interna é ΔU, de energia cinética é Δ (EC) e da energia
potencial é Δ (EP). Da primeira lei, pode-se escrever
dQ + dW = dU + dEC +dEP
Q
t

W
t

U
t

 EC
t

 EP
t
Q
lim
t  0
lim
t  0
lim
t
W
t
U
t  0
t
 Q
taxa instantânea de transferência de calor, potencia [W]
 W
taxa instantânea de transferência de trabalho, potência [W]
 U
lim
 EC
t  0
t
 E C
lim
 EP
t  0
t
 E P
Portanto a primeira lei em termos de fluxo é:
E  W  Q
U  E C  E P  W  Q
Exercício 4.1. Durante a operação de carregamento de uma bateria, a corrente
elétrica, I, é de 20 ampéres, e a tensão, e, é de 12,8 Volts, A taxa de transferência
de calor, Q , da bateria para o meio é de 10 W. Qual a taxa de aumento de energia
interna?
E  U  E C  E P
E  U  W  Q
2
W  R * i   V * i  12 , 8 * 20  256 W
U  256 , 0  10  246 , 0 W
Lei da Conservação da Massa
dm VC

dt
m VC 

m e 

e
 dm
VC
m s
m e   v e A 
ve A
v
s
VC

  dV
VC
dm VC
dt

d
dt
 Q e 
 dm
VC
m s   v s A 
VC
vs A 
Qs 
v
Fórmula Geral da Equação da Massa
d
dt
 
  v .n dA  0
 dm VC 
VC
VC
V constante na seção ( v media )
 
  v .n dA   v . A
VC
Balanço de massa em regime permanente
 m
 
  v .n dA  0
e
e
  m s  0
s
VC
Balanço de massa em regime permanente ( fluido compressível )
 m
e
e

 m
s
s

  .v . A    .v . A  0
e
s
 v .A   v .A   Q
e
s
e
e

Q
s
s
0
Exercício 4.2. Ar está escoando no interior de um tubo de 0,2 m de diâmetro à
velocidade uniforme de 0,1 m/s. A temperatura e a pressão são 25 oC e 150 kPa.
Determinar a taxa mássica, ou vazão mássica.
Exercício 4.3. Um tanque de água cilíndrico com 1,2 m de altura e 0,9 de diâmetro
, aberto, encontra-se inicialmente cheio de água. Abrindo-se uma tampa na parte
inferior do tanque permite-se que saia um jato de água com diâmetro de 13 mm .
Determinar o tempo necessário para que o nível do tanque atinja 0,6 m , medido a
partir do fundo do tanque,
Exercício 4.4. Uma mangueira de jardim conectada a um bocal é usada para
encher um balde de 10 galões. O diâmetro da mangueira é de 2 cm e ele se reduz a
0,8 cm na saída do bocal. São necessários 50 s para encher o balde com água.
Nessas condições determine: as vazões volumétrica e mássica de água através da
mangueira a velocidade de média na saída do bocal.
Primeira lei da termodinâmica a num
sistema aberto
dE sistema
dt
dE sistema
dt
 Q  W
VC

 
1

   u  V
 t  VC 
2
2


 gz   d   



 
1 2


 Q  W e
   u  V  gz   d   
 t  VC 
2


 E VC
 Q  W e

dt
t
dE
 E VC
Q VC  W e 

t
1

h


SC  2 V

2
1

u  V
SC
2


2

 gz  pv    V  n dA

1 2


 h  V  gz    V  n dA
SC
2




 gz    V  n dA

1 2


h

V s  gz s m saída 
 s
2



1 2


h

V e  gz e m entrada
 e
2


Transporte de energia pela massa
eu
1
v  gz
2
2
1 2


E massa  m .e  m  u  v  gz 
2


1 2


E massa  m e  m . u  v  gz 
2


E me 
1 2


e
dm

h

V

gz
m e

s 
 e e  s 2 s

me
Exercício 4.5. Vapor escapa de uma panela de pressão de 4 l , cuja pressão
interna é de 150 kPa. Observa-se que a quantidade de líquido da panela diminui em
0,6 l por minuto , quando são estabelecidas condições de operação estáveis. Sabese que a seção transversal da abertura de saída é de 8 mm2 . Para essas condições
determinar: a) o taxa mássica e a velocidade do vapor na saída; b) as energias
total e de escoamento por unidade de massa de vapor; c) a taxa de saída de
energia da panela.
Taxa de variação de energia para processo em regime
permanente e com escoamento unidimensional.
Q VC  W e 

1 2


h

v

gz
m saída 
 s
s
s 
2


dm VC
dt

 m
e
e
  m s
s

1 2


q m  w m     h s  v s  gz s  
2



q VC 
Q VC
W VC 
q VC
m
m
 m
e

e

1 2


h

v

gz
m entrada
 e
e
e 
2


  m s  0
s
1 2


 h e  v e  gz e  
2


Exercício 4.6
Dispositivos de Engenharia com escoamento em regime
permanente.
A. Turbinas e compressores.
Compressor, W ou w >0
Turbina , W ou
w
<0
Exercício 4.7. Ar a 100kPa e 280 K é comprimido em regime permanente até atingir
600 kPa e 400 K. O vazão mássica do ar é 0,02 kg/s e sabe-se que ocorre uma perda
de calor de 16 kJ/kg durante o processo. Considerando que as variações de energia
potencial e cinética são desprezíveis, determinar a potência consumida pelo
equipamento.
Exercício 4.8. A potencia gerada por uma turbina adiabática é de 5 MW e as
condições de entrada e saída estão indicadas na tabela ao lado. Com base nessas
informações:
a)comparar as magnitudes das grandezas Δh, Δec, Δep;
b)determinar o trabalho realizado por unidade de massa de vapor que escoa pela
turbina;
c) calcular o vazão mássica de vapor.
Entrada Saída
P(MPa)
2
0,015
T(oC)
400
-
V(m/s)
50
180
Z(h)
10
6
y
-
0,90
;
Exercício 4.9. O fluxo de massa que entra em uma turbina a vapor d'água é de 1,5
kg/s e o calor transferido da turbina para o meio é de 8,5 kW. São conhecidos os
seguintes dados para o vapor de água que entra e sai da turbina:
Determinar a potência fornecida pela turbina.
Regime permanente,
dE sistema
 0
 E VC
 0
t
dt
Primeira lei da termodinâmica

Q VC 

m 

1 2


W e  m    h s  V s  gz s  
2





m e 

m s
1 2


 h e  V e  gz e  
2



1 2
1 2
 

Q VC  W e  m   h s  V s  gz s    h e  V e  gz e  
2
2
 


Do dados do problema, Q v c =-8,5kW

1 2
1 2
 

W e  m   h s  V s  gz s    h e  V e  gz e    Q VC
2
2
 


B. Trocadores de calor.
Exercício 4.10
C. Escoamento em tubos e dutos.
Exercício 4.11
Processos de Estrangulamento e o Coeficiente de Joule Thomson
A. Válvulas de estrangulamento .
Dispositivos que restringem o escoamento e causam queda significativa
de pressão . A queda de pressão é quase sempre acompanhada por queda
na temperatura . A magnitude da queda ( ou eventual aumento da
temperatura , depende de uma propriedade dos fluidos
chamada
coeficiente de Joule-Thomson.
São dispositivos adiabáticos( Q =0 ), nos quais não há exportação ou
importação de trabalho (W=0) e variação de energia potencial é
desprezível ( Δep =0).
1 2
1 2


q m  w m   h s  v s  gz s  h e  v e  gz e 
2
2


hs 
1 2

2
v s   he  v e   0
2
2


1
h s  he
Se vs ~ ve
Dispositivo isoentálpico
 T 
 T 
J  



  P  h  cons tan te   P  Isoentalpi co
(Coeficiente de Joule-Thomson)
Se há diminuição de pressão, há diminuição de temperatura, se µJ >0;
Se há diminuição de pressão, há aumento de temperatura, se µJ <0; (hidrogênio, H2 e o
hélio, He)
Para um valor nulo do coeficiente de Joule Thomson, temos o denominado ponto de
inversão. A ilustra essas observações, onde se nota que o lugar geométrico definido
por todos os pontos de inversão constitui a curva de inversão.
Gráfico T x P, mostrando o Comportamento do Coeficiente de Joule-Thomson.
Exercício 4.12. O fluido refrigerante 134a entra no tubo capilar de um refrigerador
com liquido saturado a 0,8 MPa e é estrangulado e a sua pressão na saída é 0,12 MPa.
Determinar o título do fluido no estado final e a qual a queda de temperatura.
Processos de Estrangulamento e o Coeficiente de Joule Thomson
B. Bocais e difusores .
Exercício 4.13 . Provar que são dispositivos isoentálpicos.
Exercício 4.14 . Ar entra a 10 oC e 80 kPa no difusor de um motor a jato com
velocidade de 200m/s . A área de entrada do difusor é 0,4 m2. O ar sai do
difusor com uma, velocidade muito pequena comparada à de entrada .
Determinar a) a vazão mássica de ar e b) a temperatura na saída.
Exercício 4.15. Vapor de água a 0,5 MPa e 200 oC entra em um bocal termicamente
isolado com uma velocidade de 50 m/s, e sai à pressão de 0,15 MPa e à velocidade de
600 m/s. Determinar a temperatura final do vapor e ele estiver superaquecido e o
título se for vapor úmido.
Da 1a lei da termodinâmica, regime permanente resulta
1 2


2
v s  gz s   h e  v e  gz e   0
2
2


hs 
1
hs 
1
2
v s  he 
2
1
2
ve
2
Análise de uma unidade geradora .
Exercício 4.16. Considere uma instalação motora a vapor simples como mostrada na
figura abaixo. Os dados na tabela referem-se a essa instalação.
Determinar as seguintes quantidades , por kg de fluido que escoa através da
unidade.
1 -Calor trocado na linha de vapor entre o gerador de vapor e a turbina
2 -Trabalho da turbina
3 -Calor trocado no condensador
4 -Calor trocado no gerador de vapor.
Como nada foi dito sobre as velocidades dos fluxos mássicos e suas posições, as
variações de energia cinética e potencial, são desprezadas. As propriedades dos
estados 1,2 e 3 podem ser lidas nas tabelas termodinâmicas, assim:
P1=2,0 MPa; T1=300 oC.
P
h1 = 3023,5 kJ/kg
T
250
2911,0
x
2902,5
1,8
1,9
2,0
P
P2=1,9 MPa; T2=290 oC
P3=15,0 kPa;
T
290
T
300
3029,2
y
3023,5
z
h2 = 3002,5 kJ/kg
y = 0,9
hl = 25,91 kJ/kg
hv = 2599,1 kJ/kg
h  1  y hl  y .hv
h 3  0 ,1 . 225 , 91  0 , 9 . 2599 ,1  2361 ,8 kJ / kg
As propriedades do estado 4 devem ser lidas da tabela de propriedades
comprimidas ou, de forma aproximada, da tabela de propriedades saturadas para
a temperatura dada. Assim
P=14,0 kPa; T = 45 oC
h4 = 188,5 kJ/kg
15 kPa
40
180,75
60
263,65
1 Calor trocado na linha de vapor entre o gerador de vapor e a turbina
Aplicando-se a 1a lei por unidade de fluxo de massa temos

1 2
1 2
 

Q VC  W e  m   h s  V s  gz s    h e  V e  gz e  
2
2
 


Q VC  m  h s  h e 
2 Trabalho da turbina
Deve-se aplicar a primeira lei à turbina para fluxo unitário. Uma
turbina é essencialmente uma máquina adiabática. Portanto é
razoável desprezar o calor trocado com o meio ambiente. Assim,

1 2
1 2
 

Q VC  W e  m   h s  V s  gz s    h e  V e  gz e  
2
2
 


W e  m  h s  h e 
3 .Calor trocado no condensador
Neste caso, não há trabalho, assim,

1 2
1 2
 

Q VC  W e  m   h s  V s  gz s    h e  V e  gz e  
2
2
 


Q VC  m  h 4  h 3 
Q VC
m
 h 4  h 3 
4. Calor trocado no gerador de vapor.
Neste caso não há realização de trabalho, e a primeira lei fica

1 2
1 2
 

Q VC  W e  m   h s  V s  gz s    h e  V e  gz e  
2
2
 


Q VC
m

 h s    h e  
h1  h 5
Na resolução, necessitamos do valor de h5, que pode ser obtido considerando um
volume de controle na bomba do sistema.
5. Trabalho na bomba
A primeira lei aplicada à bomba, com a hipótese de que o processo é adiabático,
(Q=0 ), não há transferência de calor da bomba para o meio ou vice-versa, resulta:

1 2
1 2
 

Q VC  W e  m   h s  V s  gz s    h e  V e  gz e  
2
2
 


W e  m  h s    h e 
h5  h4 
Assim para o gerador, obtém-se:
W
m
e
Portanto:
W
m
e
 h5  h4