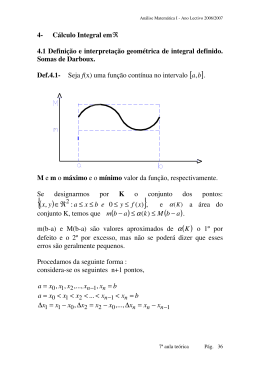
A integral definida
Seja y = f(x) uma função definida e limitada no
intervalo [a, b], e tal que f(x)  0 p/ todo x  [a, b].
Problema: Calcular (definir) a área, A, da região
do plano limitada pela curva y = f(x), o eixo OX e
as retas x = a e x = b.
Tomemos números x0, x1, x2, ..., xn  [a, b] tais
que a = x0 < x1< x2 < ... < xn = b e , a1, a2, ..., an
tais que ai  [xi-1, xi]. Então
Definição 1: Seja y = f(x) uma função definida
e limitada no intervalo [a, b]. Se existe
dizemos que f é integrável em [a, b] e que sua
integral definida em [a, b] é I e é um número
real.
Notação:
• O processo de determinação do limite é
chamado cálculo da integral
• Os números a e b são os limites de
integração; a é o limite inferior e b é o
limite superior.
• A expressão f(x) é o integrando.
Proposição: Se f (x) é contínua em [a, b] então
é integrável em [a, b].
Exemplo: f(x) = x para todo x  [0, 1].Mesmo sabendo
tratar-se de uma função que possui integral, no momento
ainda não temos recursos que facilitem calcular esta
integral. Usaremos a definição e faremos uma escolha
para os números x0, x1, x2, ..., xne a1, a2, ..., an da
seguinte forma: Dado n  N tomemos
Propriedades da integral definida
*Se f(x) e g(x) são funções integráveis em [a, b]
e k  R então f(x)  g(x) são integráveis em
[a,b] e
*k.f(x) é integrável em [a, b] e
*Se f(x)  g(x), para todo x  [a, b] então
*Se f(x)  0, para todo x  [a, b] então
Definição 2:
então
2.2) Se f(x) é integrável em [a, b]
Propriedade i) Sejam a, b, e c  R, se
Propriedade ii)
O Teorema da Média
Se f(x) é contínua em [a, b]
então existe pelo menos
um número c [a, b] tal
que
" Se f(x)  0, a área da
região limitada pela
curva y = f(x) e o eixo
Ox é igual a área do
retângulo de base [a, b]
e altura f(c)"
Definição 3 ( Valor médio): f(c) é o valor médio
de f em [a, b].
Propriedade iii)
Se f(x) é contínua em [a, b] então
é uma primitiva de f(x).
Isto é, F´(x)= f(x).
Prova:
X 
f ( )d

F ( x   ) - F ( x)
 X


Z ( X , X   )
LIM f ( Z )  LIM f ( Z )  f ( X )
 0
ZX

f(Z)

O Teorema fundamental do cálculo
Se f(x) é contínua em [a, b] e F(x) é uma
primitiva qualquer de f(x) então
b
f
(
x
)
dx

F
(
X
)

F
(
b
)
F
(
a)

a
b
a
Prova:
X
A
A
A
 f ( )d  F ( X )  C  f ( )d  F ( A)  C  C  -F ( A)
X
 f ( )d  F ( X ) - F ( A)
A
X B
Proposição 1: Sejam J um intervalo e g: [a, b]  J uma
função com derivada contínua e f : J  R uma função
contínua. Então,
Propriedade i) Se f(x) é uma função par e contínua em
[-a, a] então
Propriedade ii) Se f(x) é uma função ímpar e contínua
em [-a, a] então
Propriedade iii) Se f(x) é uma função contínua em R e
periódica de período T então para todo a Î R temos
Cálculo de áreas de figuras planas
(coordenadas cartesianas)
Observação 1:
Dada f(x) uma função
contínua em [a,b], se A é
a área da região do
plano cartesiano limitada
pelo eixo Ox e pela curva
y = f(x) e tal que a  x  b
então
Observação 2: Dadas f e g funções contínuas
em [a,b], se A é a área da região do plano
cartesiano limitada pelas curvas y = f(x) e y = g(x)
e tal que a  x  b então
Exemplo : Calcular a área da figura do plano limitada pelas curvas