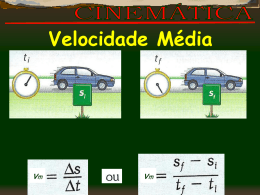
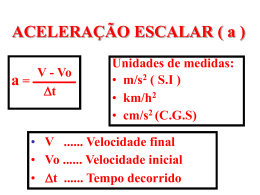
“A gravidade explica os movimentos dos planetas, mas não pode
explicar quem colocou os planetas em movimento. Deus governa
todas as coisas e sabe tudo que é ou que pode ser feito.”Isaac Newton
Prof. Dolhavan
FÍSICA
9ºano
CONCEITOS BÁSICOS
DA CINEMÁTICA
DIVISÕES PEDAGÓGICAS DA FÍSICA:
- MECÂNICA
(movimentos)
- TERMOLOGIA
(calor)
FÍSICA
- ÓPTICA
(luz)
- ONDULATÓRIA
(ondas)
- ELETRICIDADE
(energia elétrica)
- CINEMÁTICA
(efeitos)
- DINÂMICA
(causas)
- ESTÁTICA
(equilíbrio)
MECÂNICA
- Área da Física que estuda os movimentos.
Foi dividida em:
CINEMÁTICA: estuda o movimento dos corpos sem
enfocar sua causa, procurando investigar o que está
acontecendo durante esse movimento: posição,
tempo, velocidade, etc.
DINÂMICA: procura investigar suas causar, ou seja,
o porquê de um movimento estar ocorrendo.
- O primeiro cientista a se dedicar ao estudo da
Mecânica foi Galileu Galilei , embora Aristóteles
(384 a.C.) filósofo grego, já tivesse feito algumas
observações a respeito dos movimentos dos astros e
da queda de corpos.
- Seus estudos tiveram continuidade com Isaac
Newton, que por coincidência nasceu no ano da
morte do Galileu (1642-1727).
CINEMÁTICA:
É a parte da Física, dentro da Mecânica, que estuda as
consequências dos movimentos dos corpos, tais como
deslocamento, velocidade, aceleração e tempo gasto.
Para compreendermos essas consequências precisamos,
antes, conhecer alguns conceitos básicos. São eles:
- Móvel
- Trajetória
- Referencial
- Ponto Material
- Movimento
- Corpo Extenso
- Repouso
- Posição e Deslocamento
MÓVEL:
É qualquer corpo que pode se movimentar em
relação a um referencial adotado. Por exemplo: um
automóvel em relação à Terra. É importante
salientar que um móvel não é um objeto que
efetivamente se desloque, ou seja, que não esteja fixo
no chão.
Fisicamente, qualquer coisa pode ser considerada
como móvel. Por exemplo: o prédio dessa escola está
em movimento em relação ao Sol, portanto o prédio,
apesar de estar fixo no solo, pode ser considerado
um móvel.
REFERENCIAL:
O estudo do movimento de um corpo depende sempre do
referencial escolhido. Chamamos de referencial a todo ponto
que adotamos como referência para estudar o movimento
dos corpos. Podemos associar esse ponto a um corpo ou local
do espaço. Em princípio podemos adotar qualquer
referencial para descrever um movimento.
Para definirmos se um móvel está ou não em movimento
precisamos comparar sua posição com a posição de um
referencial.
Não há como saber se um corpo está ou não em movimento
se não houver um ponto de referência para a comparação.
Esse ponto de referência é chamado simplesmente de
referencial.
REFERENCIAL:
Por exemplo: a Terra está em movimento em relação ao Sol
(nesse caso, a Terra é o móvel e o Sol é o referencial
adotado).
Quando dois referenciais não aceleram nem giram um em
relação ao outro, são chamados de referenciais inerciais.
Caso contrário, serão chamados de referenciais não
inerciais.
Quando a situação não especificar o referencial a ser
utilizado, considere sempre a Terra ou o solo. Por exemplo,
se em uma situação genérica for feita uma afirmação do tipo
“um corpo se movimenta com velocidade de 80 km/h”,
considere que essa velocidade é medida em relação à Terra
ou ao solo.
MOVIMENTO E REPOUSO:
Um corpo está em movimento quando sua posição
mudar, com o decorrer do tempo, em relação ao
referencial adotado. Por exemplo: um carro com
velocidade de 80 km/h está em movimento em relação a
um poste fixo na rua, pois a posição do carro em relação
ao poste varia com o passar do tempo.
Um corpo está em repouso quando sua posição não
mudar, no decorrer do tempo, em relação ao referencial
adotado. Por exemplo: uma pessoa sentada no banco de
um veículo que se movimenta com velocidade de 80
km/h está em repouso em relação ao banco em que está
sentada, pois a sua posição não varia em relação ao
banco com o passar do tempo.
MOVIMENTO E REPOUSO:
Observe que os conceitos de repouso e de movimento
são relativos a um referencial adotado. Note ainda que é
possível o mesmo objeto estar em repouso e em
movimento ao mesmo tempo, basta considerarmos
referenciais diferentes.
Por exemplo: considere uma pessoa sentada na poltrona
de um avião que está em pleno vôo. Podemos dizer que
a pessoa está em repouso em relação às poltronas do
avião, por outro lado, podemos dizer também que ela
está em movimento em relação ao solo.
PORTANTO, NÃO EXISTE MOVIMENTO OU REPOUSO
ABSOLUTO.
TRAJETÓRIA
A trajetória mostra o caminho pelo qual um móvel irá
passar ou o caminho no qual ele passou à partir do
momento em que entrou em movimento em relação a um
referencial.
Num mesmo movimento, adotando-se referenciais
diferentes podemos encontrar trajetórias diferentes.
Por exemplo: um avião em movimento retilíneo e com
velocidade
constante
abandona
uma
bomba.
Desprezando-se o efeito da resistência do ar, a trajetória
dessa bomba será retilínea para um observador localizado
no interior do avião e parabólica para um observador em
repouso na Terra.
À medida que a bomba cai o avião se desloca para
frente. Assim, se uma pessoa dentro do avião olhar
para baixo verá a bomba cair em linha reta, ao passo
que um observador parado no chão verá a bomba cair
em forma de um arco parabólico.
PONTO MATERIAL:
Um corpo é considerado como um ponto material
quando as suas dimensões forem desprezíveis em
relação à sua trajetória ou ao local onde ele se encontra.
CORPO EXTENSO:
Um corpo é considerado como um corpo extenso
quando as suas dimensões não forem desprezíveis em
relação à sua trajetória ou ao local onde ele se encontra.
Por exemplo: um carro. Se o local de referência for a
garagem de sua casa, ele será um corpo extenso. Se o
local de referência for a extensão da rodovia
Anhanguera, ele será um ponto material.
ESPAÇO OU POSIÇÃO (S):
Chamamos de posição ao local ocupado pelo corpo em
relação a um dado referencial, num dado instante.
É um número associado à posição do móvel na
trajetória. Ele não diz se o móvel está em movimento ou
em repouso e nem quanto o móvel se deslocou, ou
mesmo se foi à favor ou contra a trajetória.
A única informação concreta dada pela posição S de um
móvel é a que distância o móvel se encontra da origem
dos espaços naquele instante. A origem dos espaços é
sempre dado por S = 0.
Placa quilométrica no km 37 de
uma rodovia. Ela está a 37 km do
marco zero dessa rodovia.
Se um veículo está no km 37
da Rodovia Cândido
Portinari, não sabemos em
que sentido ele está se
movendo ou mesmo se ele
está em movimento, pois ele
pode inclusive estar parado.
A única informação real que a posição S nos dá é de fato
onde o veículo se encontra naquele exato momento. E
essa posição é sempre tomada com referência à origem
da trajetória, ou seja, o marco quilométrico zero (S = 0).
DESLOCAMENTO ESCALAR (S):
O deslocamento escalar é a variação de posição sofrida
por um móvel sobre uma trajetória. Trata-se de uma
simples comparação entre a posição final e a posição
inicial do móvel em um trajeto qualquer.
Para calcularmos o deslocamento escalar de um móvel
não nos preocupamos com o trajeto do móvel, ou seja,
não nos interessa por onde o móvel passou, só nos
interessa o lugar onde ele começou (posição inicial) e o
lugar onde ele terminou (posição final).
O deslocamento escalar corresponde à diferença entre a
posição final e a posição inicial do móvel, no intervalo de
tempo (pontos) escolhido.
DESLOCAMENTO ESCALAR (S):
S = S – So
S = Deslocamento escalar
S = Posição final do móvel
S0 = Posição inicial do móvel
É importante ressaltar que deslocamento escalar e
distância percorrida são conceitos diferentes. Enquanto
o deslocamento escalar é uma simples comparação entre
a posição inicial e a posição final, a distância percorrida
é a soma de todos os espaços percorridos pelo móvel.
Exemplo: Considere a trajetória dada na figura abaixo. Em
cada item a seguir determine o deslocamento escalar e a
distância percorrida:
Essa trajetória está numerada de um em um metro. A origem da
trajetória é o marco zero. A trajetória é orientada positivamente
para a direita. As posições dos pontos são as seguintes:
SA = – 7m
SB = – 3m
SD = + 2m
SE = + 6m
SC = 0 (está na origem)
a) Trajeto ABD:
Nesse caso o móvel saiu da posição A, foi até a posição B e
em seguida dirigiu-se à posição D.
Deslocamento Escalar:
S = S – S0 = SD – SA = 2 – ( – 7) = 9 m
Distância Percorrida:
Entre A e B, o móvel andou 4m. Entre B e D, andou 5m.
Portanto: Distância percorrida = 9 m
b) Trajeto BED:
Nesse caso o móvel saiu da posição B, foi até a posição E e
em seguida dirigiu-se à posição D.
Deslocamento Escalar:
S = S – S0 = SD – SB = 2 – ( – 3) = 5 m
Distância Percorrida:
Entre B e E, o móvel andou 9m. Entre E e D, andou 4m.
Portanto: Distância percorrida = 13 m
c) Trajeto EAB:
Nesse caso o móvel saiu da posição E, foi até a posição A e em
seguida dirigiu-se à posição B.
Deslocamento Escalar:
S = S – S0 = SB – SE = – 3 – 6 = – 9 m
Distância Percorrida:
Entre E e A, o móvel andou 13m. Entre A e B, andou
4m. Portanto: Distância percorrida = 17 m
d) Trajeto ABA:
Nesse caso o móvel saiu da posição A, foi até a posição B e
em seguida dirigiu-se novamente à posição A.
Deslocamento Escalar:
S = S – S0 = SA – SA = – 7 – (– 7) = 0 m
Distância Percorrida:
Entre A e B, o móvel andou 4m. Entre B e A, andou 4m.
Portanto: Distância percorrida = 8 m
OBSERVAÇÕES IMPORTANTES:
- O deslocamento escalar será positivo quando o móvel se deslocar
mais no sentido positivo do que no sentido negativo da trajetória;
- O deslocamento escalar será negativo quando o móvel se deslocar
mais no sentido negativo do que no sentido positivo da trajetória;
- O deslocamento escalar será nulo em duas situações: quando o
móvel permanecer em repouso e quando ele retornar à posição
inicial;
- A distância percorrida somente será igual ao deslocamento
escalar em duas situações: quando o móvel permanecer em
repouso e quando o móvel caminhar somente no sentido positivo
da trajetória, sem voltar.
VELOCIDADE ESCALAR MÉDIA:
É a relação entre o deslocamento escalar e o tempo gasto na
sua realização. Pode ser dada em m/s, km/h, cm/s etc. A
velocidade escalar média não depende da forma da trajetória
(retilínea ou curvilínea). Só depende das condições no início e
no final do movimento considerado, e do tempo gasto na sua
realização. Matematicamente podemos calcular a velocidade
média pela seguinte expressão:
Vm = Velocidade escalar média
S = Deslocamento escalar
t = Tempo gasto
Observe que a velocidade escalar média é dada pela razão
entre o deslocamento escalar e o intervalo de tempo, e não
como usamos no cotidiano, fazendo a razão entre a distância
efetivamente percorrida e o intervalo de tempo.
Isso significa que a velocidade média pode ser positiva,
negativa ou mesmo nula, pois depende do valor do
deslocamento escalar. Assim:
S > 0, então Vm > 0. O móvel se desloca a favor da
orientação da trajetória. Movimento Progressivo.
S  0, então Vm  0. O móvel se desloca contra a
orientação da trajetória. Movimento Retrógrado.
S = 0, então Vm = 0. O móvel permaneceu parado ou o
móvel se deslocou e retornou ao ponto inicial.
IMPORTANTE:
No Sistema Internacional de Unidades (SI) a unidade de
velocidade é m/s (metros por segundo). Entretanto,
estamos mais acostumados a utilizar o km/h
(quilômetros por hora). Então, é importante saber
transformar de uma unidade para a outra. Para fazer
esta transformação adotamos a seguinte regra:
x 3,6
Por exemplo:
Km/h
m/s
72 km/h = 20 m/s (dividir 72 por 3,6)
30 m/s = 108 km/h (multiplicar 30 por 3,6)
 3,6
Movimento Retilíneo Uniforme
(MRU)
• Caracteriza-se por percorrer distâncias iguais em
intervalos de tempos iguais, ou seja, o módulo do vetor
velocidade é constante e diferente de zero.
• A aceleração do móvel é nula.
• Função utilizada no MRU:
S = So + Vt
S = posição final
So = posição inicial
V = velocidade do móvel
t = tempo
Gráficos do MRU
1º: Posição x Tempo
• Movimento progressivo: Velocidade positiva, isto é,
o móvel
desloca-se no sentido positivo da trajetória.
• Movimento regressivo: Velocidade negativa, isto é, o móvel
desloca-se no sentido negativo da trajetória.
Gráficos do MRU
2º: Velocidade x Tempo
PROPRIEDADES NOS GRÁFICOS DE MRU
1º: Posição x Tempo
PROPRIEDADES NOS GRÁFICOS DE MRU
2º: Velocidade x Tempo
Movimento Retilíneo Uniformemente Variado
(MRUV)
• Movimento cuja velocidade varia uniformemente no decorrer do
tempo, isto é, varia de quantidades iguais em intervalos de tempos
iguais.
• A aceleração do móvel é constante no decorrer do tempo e
diferente de zero.
• O espaço percorrido aumenta proporcionalmente ao quadrado do
tempo.
• Funções utilizadas no MRUV:
V = Vo + at
S = So + Vot + at2
2
V2 = Vo2 + 2aΔS (equação de Torricelli)
a = ΔV/Δt
Gráficos do MRUV
1º: Posição x Tempo
 Concavidade voltada para cima = aceleração positiva
 Concavidade voltada para baixo = aceleração negativa
Gráficos do MRUV
2º: Velocidade x Tempo
 Velocidade e aceleração com sinais iguais = movimento acelerado
 Velocidade e aceleração com sinais diferentes = movimento retardado
Gráficos do MRUV
3º: Aceleração x Tempo
PROPRIEDADES NOS GRÁFICOS DE MRUV
1º: Velocidade x Tempo
PROPRIEDADES NOS GRÁFICOS DE MRUV
2º: Aceleração x Tempo