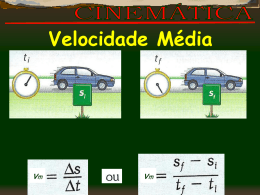
Por
Marcos Germano Degenhardt
DEFINIÇÃO
É a parte da mecânica que trata dos
movimentos dos corpos sem levar em
consideração as causas que os originam.
CONCEITOS IMPORTANTES
REFERENCIAL
Por referencial entende-se qualquer
corpo ou objeto a partir do qual se
localiza um objeto ou um móvel.
REPOUSO
Tem-se um repouso quando um móvel
no decorrer do tempo não muda de
posição em relação ao referencial.
Notar que durante os 10
segundos, o móvel permaneceu
na mesma posição.
MOVIMENTO
Tem-se um movimento quando um
móvel no decorrer do tempo muda sua
posição em relação ao referencial.
Perceber que o móvel deslocouse de uma posição situada a 10m
do referencial para outra situada
a 20m do mesmo, enquanto se
passaram 10s.
Ilustrações
Os dois filmes abaixo ilustram melhor os
conceitos de repouso e de movimento no
decorrer do tempo.
Clique nas
figuras para
visualizar os
movimentos
REPOUSO
O tempo passa e a
posição do móvel
não se altera
MOVIMENTO
O tempo passa e a
posição do móvel
se altera
TRAJETÓRIA
É o conjunto de posições pelas quais um
móvel já passou ou poderá passar. Quando
todos estes pontos são unidos formam uma
linha, e esta representa a trajetória.
Classificação das trajetórias
As trajetórias podem ser:
Retilíneas
Circulares
Parabólicas
Clique nas figuras para visualizar os movimentos
DESLOCAMENTO
Há um deslocamento toda vez que o móvel
se afastar (ou aproximar) do referencial. Este
deslocamento é medido em metros, sendo
calculado por:
x  x1  x0
Onde:
x
x1
x0
Deslocamento
posição final
posição inicial
Exemplo
Numa viagem de automóvel, uma pessoa observa que,
quando entra na auto-estrada, encontra-se no quilometro
105 e quando chega ao seu destino está no quilômetro 287.
Qual a distância percorrida durante a viagem?
Solução
A distância percorrida corresponde a diferença entre as
duas posições: inicial e final. A posição inicial é de entrada
na auto-estrada (x0=105 km) e a posição final é a de chegada
(x1=287 km).
x  x1  x0  287 km 105km  182km
VELOCIDADE
É a grandeza que exprime qual a distância
que um móvel percorre em um intervalo
unitário de tempo.
É calculada por:
v 
Onde:
v
x
t
x
t
velocidade
deslocamento
intervalo de tempo
Classificação dos movimentos
quanto a velocidade
O móvel avança da posição
de menor valor para a de
maior valor, afastando-se
assim do referencial no
sentido positivo do eixo x:
O móvel avança da posição
de maior valor para a de
menor valor, afastando-se
assim do referencial no
sentido negativo do eixo x:
Movimento
PROGRESSIVO
Movimento
RETROGRADO
Unidades da velocidade
Conversão entre as unidades:
m
km
1  3,6
s
h
Exemplos
Primeiro Exemplo
Um veículo no instante t0 = 2 s passa pelo ponto A
e no instante t1= 7 s passa pelo ponto B de uma
trajetória retilínea. Qual sua velocidade?
Solução
x x  x0 300 100 200
m
v



 40
t t  t0
72
5
s
Segundo Exemplo
Um veículo desloca-se a 108 km/h. Qual sua
velocidade em m/s?
Solução:
Como 1 m/s = 3,6 km/h, então:
1 m/s — 3,6 km/h
x m/s — 108 km/h
logo: x * 3,6  108*1
108
m
x
 30
3,6
s
Terceiro Exemplo
A distância do Sol até a Terra é de 150 milhões
de quilômetros. Se a velocidade da luz for tida
como 300 000 km/s, quanto tempo demora para
a luz solar atingir a Terra?
Solução:
x
x
v
ent ãot 
t
v
x 150000000
t 

 500s
v
300000
500s equivalem a 8 min 20 s.
ACELERAÇÃO
É a grandeza que informa quanto a
velocidade varia - aumenta ou diminui num intervalo unitário de tempo.
Obtém-se a aceleração por:
v
a
t
Onde:
a
v
t
Aceleração;
Variação da velocidade; e,
Intervalo de tempo.
Na animação a seguir, tem-se um móvel,
inicialmente em repouso, cuja velocidade aumenta
progressivamente no decorrer do tempo:
Clique na figura para
visualizar o movimento
Repare que, quanto mais o tempo
passa, mais a velocidade aumenta
Classificação dos movimentos
quanto a aceleração
Há dois casos a considerar:
A velocidade do móvel
aumenta no decorrer do tempo:
Movimento
A velocidade do móvel
diminui no decorrer do tempo:
Movimento
ACELERADO
DESACELERADO
Ilustração
Observar que o móvel, no início da
contagem do tempo tem velocidade
de 10 km/h.
Sendo acelerado constantemente,
sua velocidade aumenta para 60
km/h em 1 minuto e 30 segundos.
Unidade da aceleração
Exemplos
Primeiro Exemplo
Qual a aceleração de um móvel, cuja
velocidade aumenta de 5 m/s para 25 m/s em
4 segundos?
Solução
v v  v0 25  5 20
m
a



5 2
t
t
4
4
s
Segundo Exemplo
O maquinista de um trem aciona os freios da
composição reduzindo sua velocidade de 40 km/h
para 30 km/h em 1 minuto. Qual a desaceleração do
trem?
Solução
km
km
km
40
 30
10
v
km
h
h
h
a


 600 2
1
t
1 min
h
h
60