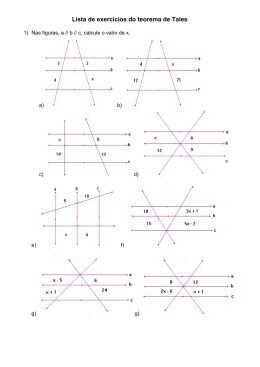
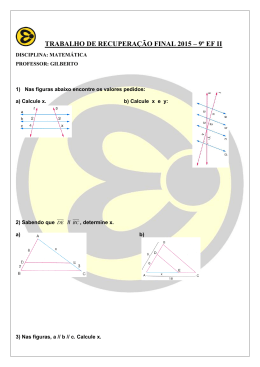
COLÉGIO MACHADO DE ASSIS
Disciplina: Matemática
Professor: Alexandre Machado Vieira
Turma: 9º ano ___
Data:
Aluno(a):
Nº:
ESTUDO DE RECUPERAÇÃO 2º TRIMESTRE
1) Nas figuras, a // b // c, calcule o valor de x.
a)
b)
c)
e)
f)
/
d)
e)
g)
/
2) Determine x e y, sendo r, s, t e u retas paralelas.
a)
b)
c)
d)
3) Determine x e y, sendo r, s e t retas paralelas.
BC de um triângulo ABC determina o ponto D em AB e E em AC . Sabendo –
se que AD = x, BD = x + 6, AE = 3 e EC = 4, determine o lado AB do triângulo.
4) Uma reta paralela ao lado
5) A figura ao lado indica três lotes de terreno com frente para a rua A e para rua B. as divisas dos lotes são
perpendiculares à rua A. As frentes dos lotes 1, 2 e 3 para a rua A, medem, respectivamente, 15 m, 20 m e
25 m. A frente do lote 2 para a rua B mede 28 m. Qual é a medida da frente para a rua B dos lotes 1 e 3?
6) Um feixe de quatro retas paralelas determina sobre uma transversal três segmentos consecutivos, que
medem 5 cm, 6 cm e 9 cm. Calcule os comprimentos dos segmentos determinados pelo feixe em outra
transversal, sabendo que o segmento desta, compreendido entre a primeira e a quarta paralela, mede 60
cm.
7) As alturas de dois postes estão entre si assim como 3 esta para 5. Sabendo que o menor deles mede 6 m,
então o maior mede:
8) A figura abaixo nos mostra duas avenidas que partem de um mesmo ponto A e cortam duas ruas paralelas.
Na primeira avenida, os quarteirões determinados pelas ruas paralelas tem 80 m e 90 m de comprimento,
respectivamente. Na segunda avenida, um dos quarteirões determinados mede 60 m. Qual o comprimento
do outro quarteirão?
9) Na figura abaixo, sabe – se que
e y indicadas.
A
RS // DE e que AE = 42 cm. Nessas condições, determine as medidas x
10) Num triângulo ABC, o lado AB mede 24 cm. Por um ponto D, sobre o lado AB , distante 10 cm do vértice
A, traça – se a paralela ao lado
do lado
BC , que corta o lado AC tem 15 cm de comprimento, determine a medida
AC .
11) No triângulo ABC da figura, sabe – se que DE //
triângulo.
A
BC . Calcule as medidas dos lados AB e AC do
12) Na figura abaixo, AE // BD . Nessas condições, determine os valores de a e b.
13. (Unirio) Consideremos um ponto de luz no chão a 12m de um edifício. Numa posição entre a luz
e o edifício, encontra-se um homem de 2m de altura, cuja sombra projetada no edifício, pela mesma
luz, mede 8m.
Diante do exposto, calcule:
a) a distância entre o homem e o edifício;
b) o valor da cossecante do ângulo formado pelo facho de luz que atinge o homem.
14. (PUC-PR) A área do retângulo DEFB é:
a) 24.
b) 160.
c) 120.
d) 20.
e) 180.
15. Considerando a figura abaixo, o valor de x é igual a:
A
a) 8,5 m.

x
b) 12 m.
c) 6,5 m.
12 cm
E
d) 16 m.
e) 10,5 m.

B
D
14 cm
- EQUAÇÃOS DO 2º GRAU:
3 cm
C
7. Resolva as seguintes equações do 2º grau, identifique os coeficientes e determine as raízes se existir.
a) x² - 5x + 6 = 0
b) x² - 8x + 12 = 0
c) x² + 2x - 8 = 0
d) x² - 5x + 8 = 0
e) 2x² - 8x + 8 = 0
f) x² - 4x - 5 = 0
g) -x² + x + 12 = 0
i) -x² + 6x - 5 = 0
j) 6x² + x - 1 = 0
k) 3x² - 7x + 2 = 0
l) 2x² - 7x = 15
m) 4x² + 9 = 12x
n) x² = x + 12
o) 2x² = -12x - 18
p) x² + 9 = 4x
q) 25x² = 20x – 4
r) 2x = 15 – x²
s) x² + 3x – 6 = -8
t) x² + x – 7 = 5
u) 4x² - x + 1 = x + 3x²
v) 3x² + 5x = -x – 9 + 2x²
x) 4 + x ( x - 4) = x
z) x ( x + 3) – 40 = 0
Estudar também as questões das provas e os exercícios resolvidos da apostila.