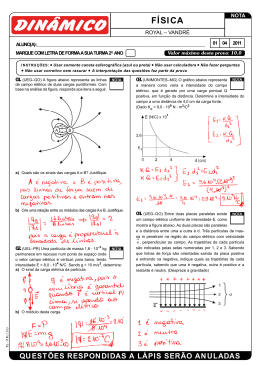
Exercícios
a
1) Calcule o campo elétrico no vértice do triângulo.
+Q
-Q
2) Duas cargas de sinais opostos (e módulo igual a 2x10-7C) estão separadas
por 15cm. Determine o vetor E no meio da reta que une as cargas e a força caso
um elétron seja colocado nesse ponto.
3) Duas cargas estão separadas por uma distância d. Que condições devem ser
satisfeitas para que em alguma região o campo elétrico seja nulo?
4) Duas cargas, uma de -5q e a outra de +2q, estão separadas por uma
distância d. Calcule o ponto onde o campo elétrico é nulo.
5) Duas cargas, uma de +2q e a outra de +4q, estão separadas por uma
distância d. Calcule o ponto onde o campo elétrico é nulo.
6) 4 cargas estão dispostas nos vértices de um quadrado de lado a. Calcule
o campo elétrico resultante no centro do quadrado (origem).
Q2= -2q
Q1 = q
Este problema , a priori, é
bastante trabalhoso, mas,
devido à simetria da
disposição das cargas, ele
pode ser resolvido de uma
forma rápida.
y
a
x
Q4= -q
a
Inicialmente vimos que a
solução é colocar uma
carga de prova no centro do
quadro, em seguida calcular
a força elétrica total e
depois dividir o resultado
pela carga de prova.
Esqueçamos isto!
Q3= + 2q
A distância entre cada carga e o centro do quadrado é sempre

E1  E4
e
E3  E4
a
2.
Q2= -2q
Q1 = q
E3
a
E3y
E4
Q4= -q
E   E1,4 .sen(450 ) 
E   E2,3 .sen(450 ) 
E1  E1x xˆ  E1y yˆ
E2
E2y
E2  E2x xˆ  E2y yˆ
E2x
E3x
E4x
E1x
E4y
E  E1  E2  E3  E4
E4   E4x xˆ  E4y yˆ
E1
E1y
E3   E3x xˆ  E3y yˆ
E4x  E1x  E4 y  E1 y  E 
E3x  E2x  E3 y  E2 y  E 
a
Q3= + 2q
kq
a 


2

k 2q
a



2

.
2
.
2
 E  ( 2E  2E) yˆ
1
2
1
2
kq
2kq
2kq


 E    2 2 2  2 2 2  yˆ  2 2 yˆ
a
a
a


Procure modificar a configuração das cargas (troque de lugar) e
discuta o que pode acontecer.
Existe alguma configuração que poderia produzir um campo resultante
sem componente x para direita.