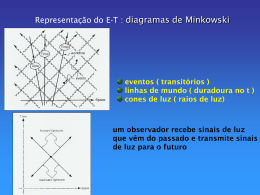
Resumo da aula anterior...
Relatividade especial
trabalha com referenciais inerciais
Bem sucedida:
1. ao obter que c é constante p/  observador
2. descrever os efeitos para v próxima a da luz
No entanto... incompatível com a teoria newtoniana da
gravitação
objetos se atraem com F dependente
da distância entre eles e esta força é
de ação instantânea (v infinita)
Einstein propôs a teoria da relatividade geral
trabalha com referenciais acelerados
Gravidade não é uma força e sim consequência que
o espaço-tempo não é plano
E-T curvo pela distribuição de massa+energia
nele contida
Teoria geral da gravitação!
Exemplo:
Terra não se desloca numa órbita curva devido
a ação da gravidade do Sol
Terra segue uma trajetória mais curta no
E-T curvo
geodésica
Terra percorre uma linha de mundo reta no E-T curvo 4D
no espaço 3D aparece como sendo uma
órbita curva
Testes da TRG
Medida da intensidade da gravidade ou curvatura:
 Vescape 

 
 c 
2
Vescape  2GM
r
Exemplo: superfície do Sol Vescape=618 km/s
intensidade ~ 4x10-6 (4 partes em 1 milhão)
Efeitos relativísticos mais importantes em curvaturas
mais pronunciadas, onde Vescape →c
vizinhanças de buracos negros
Testes de Einstein
Deflexão da luz
Experiência:
Luz de uma estrela distante passando perto do
Sol, deverá ser desviada de um ângulo pequeno
que é 2  o ângulo predito por argumentos Newtonianos
 Vescape
  2  
 c
2

 rad

1 rad = 2.06265x105 arcsec
raio de luz
visível
são observadas perto do sol somente
durante um eclipse solar...
uma das primeiras comprovações
da TRG foi durante o eclipse visto
em Sobral/Ce (1919)

 = 1.98 arcsec
Newton: 0.87 arcsec
Medidas mais precisas são feitas por radioastronomia
Redshift gravitacional
A radiação que escapa de uma estrela ou planeta
perde energia   aumenta para um observador no espaço
obs  
z

Para um obs na superfície de uma estrela ou planeta 
radiação vinda do espaço ganha energia   diminui (blueshift)
Experimento:
B
quando o fóton entra em A o lab começa a cair
h
A
g
o fóton ultrapassa chega em B
dentro do lab  é constante
(efeito da gravidade é anulado)
Redshift gravitacional
A radiação que escapa de uma estrela ou planeta
perde energia   aumenta
obs  
z

Se a curvatura do E-T não
for importante (campo grav. fraco)
aproximações não-relativísticas
B
h
A
g
Quando o fotón entra em A o lab começa a cair
A variação do pot. grav.  sofrida
por um fóton em A e B:

g=-= r
= gr = gh
vel. do lab: v = -gt (em rel a um obs externo)
(no lab vale TRE) sinal leva t = h/c de A para B
v= - gh/c
gh

z



Sendo v pequena →z=v/c
c2
c2
Calculando o z gravitacional produzido por uma estrela
de massa M e raio R
A variação do  sobre um fóton da estrela até uma
distância infinita vale:    GM
R
GM
z 2
c R
Para uma anã branca (M=1M e R=109 cm) →z≈1.5x10-4
Em geral é bem menor do que o z por velocidade
Outra maneira de expressar o redshift gravitacional ...
em termos da dilatação do tempo num campo
gravitacional em vez de variação de 
Pode-se definir os períodos associados a
A e B :
t A 
B
Logo:
h
A
g
A
c
t B 
B
c
B   A t B  t A t B
z


1
A
t A
t A
Se z    
c2

t B  t A (1  2 )
c
Intervalo de tempo em B < intervalo de t em A
relógio anda mais lento em A
Quanto mais perto do objeto massivo  mais lento anda o relógio
para um observador externo
Resumindo...
>
espaço
1. A voz fica mais grave ( maior,  menor)
2. A voz fica mais lenta
>
espaço
1. A voz fica mais aguda ( menor,  maior)
2. A voz fica mais rápida
Problema...
tA e tB são tempos próprios medidos num referencial em repouso
em relação a A e B, mas como tA ≠ tB
sincronização dos relógios!!
já que potencial altera o fluxo do tempo
Os tempos devem ser expressados em termos de um observador no espaço
em um  nulo!!
mede-se então t neste ponto
Então t vai se relacionar com  num dado potencial (P):
M
P
(P)

0
=0
t
( P )
  t (1  2 )
c
Fluxo do tempo é alterado pelo potencial