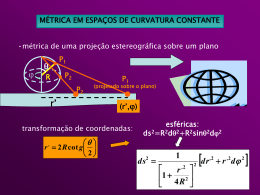
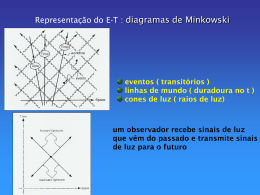
Resumo de aulas anteriores
Geodésica: menor distância entre dois pontos
• espaço euclidiano: linhas retas
• espaço esférico: arco de círculo máximo
• espaço hiperbólico: hipérbole
Um caminho descrito por um corpo livre que obedece a 1a lei
de Newton de movimento pode ser descrita expressando suas
coordenadas espaciais como função do tempo: x(t), y(t), z(t)
t absoluto
Este caminho representa a menor distância entre dois pontos
geodésica do espaço
CASO RELATIVÍSTICO: t é relativo
Supondo um espaço plano 3-D dado por dl2=dx2+dy2+dz2
Pode-se substituí-lo por um espaço-tempo 4-D de Minkowski,
definido pelas coordenadas espaciais x,y,z e pela
distância temporal ct, onde x() , y() , z() , t()
tempo próprio (absoluto)
ds2=c2dt2-|dl2|
métrica pseudo-euclidiana
a distância espacial dl entre dois pontos num espaço 3-D é
generalizada à distância ds entre dois eventos num E-T 4-D
definido pelas coordenadas de tempo e espaço
Dois eventos separados no E-T são causamente conectados
por sua separação espacial dl e temporal dt obedecendo
a lei:
dl
dt
 c
ds2=c2dt2-|dl2| , se dl/dt=c dl=cdt ds2=c2dt2-c2dt2= 0
um sinal de luz tem separação nula
ou atravessa um espaço de geodésicas
nulas (ligth-like)
O intervalo de tempo próprio d = ds/c (entre dois eventos ao longo
da linha de mundo de um corpo)
luz : d = 0
Limita o universo observável presente
contém todas as linhas de mundo que podem
ser observadas em princípio
MÉTRICA DE ROBERTSON-WALKER
Sai do caso plano (K=0), para diferentes K ou
geometrias possíveis
Mas K é sempre constante (princípio cosmológico)
Z
Geometrias
Possíveis:
Ҝ= 1/R2
R
P
X
Definição:
Ҝ= -1/R2
Y
Ҝ(t)=k / R2(t)
fator de escala ou
parâmetro de expansão
k =-1,0,+1
A curvatura é constante somente num dado t, mas varia para
tempos diferentes
Suposições:
• universo como um fluído isotrópico e homogêneo : fluído cosmológico
• descrição da posição de um objeto no espaço: coordenadas comóveis
como coordenadas
lagrangeanas
• quantidade absoluta:  = tempo próprio medido por “relógios”
em repouso em relação ao fluído cosmológico
referencial inercial
Vimos que a métrica de um espaço 3-D de Ҝ constante pode
Raio
ser descrito como:
ds2 espacial 
próprio
2
da
2
2
2
2

a
(
d


sin

d

)
2
1  a
Onde a não é o raio próprio no espaço
a
a não é comóvel
corte vertical da esfera anterior:
a

R
expandindo ou
contraindo a esfera
a muda o seu valor
mas  fica constante
adimens.
a
Podemos usar como coordenada comóvel:  
R(t )
2
da
2
2
2
2
ds2 espacial 

a
(
d


sin

d

)
 = sin
2
1  a
Substituindo na métrica r=R(t) e Ҝ=k/R2(t)
2

d

2
2
2
2
2
2
2
2
ds  c dt  R ( t )
  (d  sin  d 
2
 1  k

MÉTRICA DE ROBERTSON WALKER (MRB) (1934)
MRW : ds2 = distância entre dois eventos num E-T 4D
definidos pelas coordenadas de tempo e espaço
Ao longo da linha de mundo de um observador comóvel
(em repouso em relação a um dado ref. inercial)
ds2espacial=0  ds2=c2dt2-ds2espacial
 dds/c d=dt
Pode-se demonstrar que se (,,) = constante é uma geodésica
no E-T (todos os observadores comóveis estão em “queda livre”)
Se (,,) = constante  d=d= d=0  ds2espacial=0
 d=dt
Demonstração:
Pelo princípio da equivalência:
gravitação é considerada como um aspecto intrínseco do E-T
Campo gravitacional é uma “manifestação” da curvatura do E-T:

2
goo
4G

c2
goo determina propriedades
geométricas do E-T (ex. K)
Cada galáxia segue, além da expansão, um caminho “natural”
descrito pela geometria do E-T
movimentos de algumas galáxias são observados em direções
diferentes da direção dada pelo movimento de recessão devido à
expansão
Postulado da TRG: corpos livres movem-se ao longo de geodésicas
no E-T curvo
Se (,,) = constante é uma geodésica  referencial comóvel
 observador em “queda livre”
Sistema de coordenadas comóveis: está em repouso em
relação à matéria no universo
DEFINIÇÕES DE DISTÂNCIAS E VELOCIDADES PRÓPRIAS
em termos da MRW
Seja:
nossa galáxia →coordenadas (,,)=(0,0,0)
galáxia arbitrária → coordenadas (,0,0)
definição de D própria → dDP=cdt (no E-T ds2=0)
 d 2
2
2
2
2
ds  c dt  R ( t )


(
d


sin

d

0
2
1

k



2
2
2
2
dD2P
 d 2
2
2
2
2
dDP  R( t )
  (d  sin  d 
2
 1  k

1/ 2
Sendo  e  fixos:
 dD
P

 R(t )
0

d
1  k
2
D P  R( t ) 
0
d
1  k 2
arcsin k  1 


DP  R( t )   k  0



arcsin
h

k


1


DP depende de R que depende do t
Analisando:
1. k=0 : DP=R(t)   pode crescer sem limite com DP
Espaço plano (=a/R(t), DP=a)  universo não-ligado
2. k=+1: DP= R(t)arcsin  =sin(DP/R(t))
valor máximo de  : DP= /2R

/2R
DP
Viajando a uma distância DP=R através de um espaço
curvo 3D voltamos ao ponto de partida!!!
Universo com k>0 : ligado e fechado
3. k=-1: DP= R(t)arcsinh  =sinh(DP/R(t))
sinhx=(ex-e-x)/2

DP
 pode crescer indefinidamente com DP →
k=-1: universo não-ligado e aberto
Velocidade própria entre duas galáxias:
dDP
VP 
dt

Se DP  R(t )

0
d

1  k
2

VP  R(t )
0
d
1  k 2

Então: V  R( t ) D  H ( t ) D
P
P
P
R( t )

Onde:
R( t )
H (t ) 
R( t )
é o parâmetro de Hubble
VP=H(t)DP é uma equação semelhante à de Hubble, não
Estritamente igual pois envolvem DP e VP que não podem
Ser medidas diretamente
EQUAÇÕES DE FRIEDMANN
Obtidas a partir das equações de Einstein da TRG, usando a MRW:
8G
Gij 
Tij
4
c
Gij = tensor de Einstein : descreve a geometria do universo
Tij = tensor energia-momentum: descreve a distribuição de
matéria e energia
Distribuição de matéria+energia provoca uma curvatura no E-T
que é descrita pelas equações de Einstein
Vimos que:
campo gravitacional é uma “manifestação” da curvatura do E-T:

2
goo
4G

c2
Generalização desta equação para a TRG:
• A TRE diz que toda a forma de energia possui massa (E=mc2)
 = matéria+ energia
a generalização de  nos leva a Tij = distribuição de
matéria e energia
• generalização de  2 g para uma métrica pseudo-riemanniana
oo
arbitrária leva ao chamado tensor de
Einstein Gij que depende de gij e suas
derivadas 1a e 2a
Em cosmologia Tij vai depender de 2 funções: pressão p(t)
e densidade (t), onde p(t) é a pressão exercida num fluído
cosmológico devido à radiação + movimento peculiar das galáxias
pressão dinâmica
Então chega-se a duas equações fundamentais que
descrevem a dinâmica do universo:


8G
kc
R( t )
R( t )
p( t )  

2

2
2
2
c
R( t )
R( t )
R( t )
2
2

8G
kc2
R( t )2 
 (t ) 


2
2
3
R( t )
R( t )
3
constante
cosmológica
 → introduzida por Einstein para obter soluções para
um universo em equilíbrio
Soluções estáticas (R=cte)
Combinando as duas equações:
4G 
3 p( t ) 
1
R
  ( t )  2  R( t )  R( t )
3 
c 
3

Equação do movimento que vai definir a
expansão ou contração do universo
Estas equações nos dão: k (geometria) e R(escalas de distância)
do universo, conhecendo-se  e p.
Obtemos a equação da evolução do universo R(t)  t para uma
dada geometria
Notinha: se =0 e p=0  R   4G R

3
= cosmologia newtoniana para cte =0
No entanto R(t) tem outra interpretação...
Vê-se que não existem soluções estáticas para =0,isto é, R=cte...
por isso Einsten introduziu 