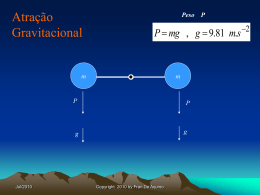
Energia Potencial e
Conservação da
Energia
Prof. Hebert Monteiro
Introdução



Imagine que você precisa realizar o trabalho de erguer uma pedra pesada
acima de sua cabeça. Parece razoável pensar que elevando essa pedra ao
ar você está armazenando energia no sistema, energia que será mais tarde
convertida em energia cinética quando a pedra cair.
Esse exemplo aponta para a idéia que deve existir uma energia associada
a posição dos corpos em um sistema.
Esse tipo de energia fornece o potencial ou a possibilidade de realização
de um trabalho sobre a pedra, que só será realizado quando a pedra for
libertada.

Por esse motivo a energia associada com a posição do objeto no sistema é
chamada de ENERGIA POTENCIAL.

A discussão sobre o assunto sugere que exista uma energia associada ao
peso do objeto e com sua altura acima do solo. Chamamos essa energia
de ENERGIA POTENCIAL GRAVITACIONAL.
2
Definindo equações

Considere um corpo de massa m que se move ao longo do eixo Y. As
forças que atuam sobre ele são seu peso (ou força gravitacional) e
possivelmente outras forças como a resistência do ar por exemplo que
chamaremos de Foutra.
3

Como podemos ver na figura anterior, o corpo realiza uma queda de uma
altura Y1 acima da origem até uma altura menor Y2 (mais próxima do solo).
O peso e o deslocamento possuem o mesmo sentido, ou seja, o trabalho
que nesse caso é chamado de Wgrav realizado sobre o corpo é positivo de
modo que:
Wgrav = F.d = (m . g) . d →
Wgrav = (m . g) . (y1 – y2) →
Wgrav = mgy1 – mgy2
4

A equação anterior nos mostra que o Wgrav varia de acordo com a
posição do objeto na queda. Essa grandeza, ou seja, o produto
entre o peso (m.g) e a altura y, denomina-se energia potencial
gravitacional.
Ugrav = m.g.y
Ugrav1 = m.g.y1
Ugrav2 = m.g.y2
Seu valor inicial
Seu valor final
Se:
Wgrav = Ugrav,1 – Ugrav,2 → - (Ugrav,2 – Ugrav,1) = - ΔUgrav
Wgrav = - ΔUgrav
5
Conservação da Energia Mecânica (somente forças gravitacionais)

Imaginem um objeto movendo-se na vertical de cima para baixo ou de
baixo para cima. A unica força atuante sobre ele é a da gravidade. Sendo
assim o objeto possui velocidade v1 quando está na posição y1 e
velocidade v2 quando encontra-se na posição y2.

O teorema do trabalho-energia visto até então diz o seguinte:
Wtot = ΔK = k2 – k1
Como a gravidade é a única força que atua sobre o corpo, de acordo com a
equação anterior:
Wtot = Wgrav = - ΔUgrav
ΔK = - ΔUgrav
6

Que pode ser escrito como:
K1 + Ugrav,1 = K2 + Ugrav,2
(Se somente a gravidade realiza trabalho)
Se chamarmos a soma da energia cinética (k) com a potencial (U) de E
(energia total do sistema), temos que:
E1 = k1 + Ugrav,1
e
E2 = k2 + Ugrav, 2
E1 = E2
(a energia total do sistema é a mesma em qualquer posição)
E = K + Ugrav
O que define e lei da conservação da energia mecânica, que diz:
A energia total de um sistema é constante, ou seja, a mesma, em qualquer
parte do movimento, variando apenas suas componentes Cinética e
Potencial.
7
Exercícios

01) Você arremessa uma bola de beisebol de 0,145 kg verticalmente de
baixo para cima, fornecendo-lhe uma velocidade incial de módulo igual a
20,0 m/s. Usando a conservação da energia, calcule a altura máxima que
ela atinge, supondo que a resistência do ar seja desprezível.
8

2) Certo dia uma escaladora de montanhas de 75 kg sobe do nível de 1500
m de um rochedo vertical até o topo a 2400 m. No dis seguinte, ela desce
do topo até a base do rochedo, que está a uma elevação de 1350m. Qual é
a variação da energia potencial gravitacional dela: a) no primeiro dia; b) no
segundo dia?
9
Quando outras forças, além da gravidade, realizam trabalho

Se outras forças além do peso atuam sobre o corpo, então Foutra não é
igual a zero, como vimos nos exemplos anteriores. Nesse caso o trabalho
exercido pela força da gravidade continua o mesmo, más o trabalho total
(Wtot) é dado agora pela soma de Wgrav com o trabalho realizado pela
Foutra.
Wtot = Wgrav + Woutra
Wgrav + Woutra = K2 – K1
Ugrav,1 – Ugrav,2 + Woutra = K2 – K1
K1 + Ugrav,1 + Woutra = K2 + Ugrav,2
10
Energia Potencial gravitacional para movimentos ao longo de
uma trajetória curva.


Quando a trajetória é curva,
também atuam sobre o corpo a
força gravitacional p = m.g e
possivelmente também outras
forças
que
possuem
uma
resultante chamada Foutra.
Sendo assim, concluimos que
podemos utilizar as mesmas
expressões para energia potencial
gravitacional tanto para uma
trajetória retilínea quanto para
uma trajetória curva, ou seja, o
trabalho realizado pela força
gravitacional depende somente da
diferença de altura entre os dois
pontos da trajetória.
11
Exercício

1) Seu primo Tobias pratica Skate deslocando-se para baixo de uma rampa
circular em um playground. Se considerarmos Tobias e seu skate como
uma partícula, seu centro se move ao longo de um quarto de círculo de raio
R = 3,00 m. A massa total de Tobias e seu skate é igual a 25,0 kg. Ele parte
do repouso e não existe nenhum atrito. a) Calcule sua velocidade na parte
inferior da rampa.
12
Resolução
13
Um círculo vertical com atrito.

2) Imaginemos o exercício anterior, porem, considerando a existência de
uma força de atrito f que realiza trabalho. Nesse caso, o trabalho não
gravitacional realizado sobre Tobias entre os pontos 1 e 2, Woutra, é
diferente de zero. Considere a velocidade de Tobias na base da rampa
sendo 6 m/s. Encontre o trabalho realizado pela força de atrito.
14
Um plano inclinado com atrito

3) Uma caixa de 12 kg está em
repouso sobre o solo. Desejamos
levá-la até um caminhão fazendo-a
deslizar 2,5 m sobre uma rampa
inclinada 30º. Um trabalhador,
ignorando o atrito, calculou que ele
poderia fazer a caixa chegar ao topo
da rampa lançando-a com uma
velocidade inicial de 5,0 m/s na base
da rampa. Porém, o atrito não é
desprezível; a caixa desliza 1,6 m
subindo a rampa, pára e desliza
retornando para baixo. a) Supondo
que a força de atrito seja constante,
calcule o seu módulo. b) Qual a
velocidade da caixa quando ela
atinge a base da rampa?
15
Resolução
16