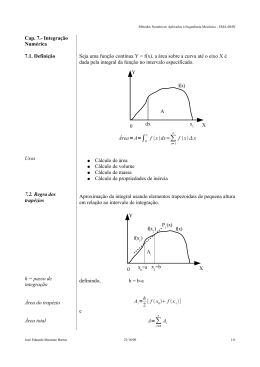

Análogo do que foi feito, aproximando f(x) por um
P1(x) (Regra do Trapézio), pode-se também
aproximar f(x) por um polinômio de grau 2, i.e. um
P2(x).
a = x0

x1
b = x2
Subdividimos
o
intervalo
(a,b)
em
dois
subintervalos iguais e fazemos a=x0, b=x2 e o
ponto médio entre (a,b) igual a x1.
a = x0
x1
b = x2

Assim:

Utilizando a fórmula de Lagrange de Grau 2.

Exemplo: Calcular
x
f(x)
pela regra do 1/3 de Simpson.
1
1
2,5
1/2,5
4
1/4
Erro de Truncamento da Regra do 1/3 de Simpson


O limitante Superior do erro da integração usando a
regra do 1/3 de Simpson é calculado por:
Apesar de se basear na interpolação de um P2(x), a
regra do 1/3 de Simpson integra sem erro um
polinômio de grau 1, 2 e 3.
Regra do 1/3 de Simpson para m intervalos
Regra do 1/3 de Simpson para m intervalos

Logo:

Onde m = n° de subintervalos.

Obs.: A regra do 1/3 de Simpson só funciona com m par.
Limitante Superior do Erro de Truncamento

O limitante Superior do erro da integração usando a
regra do 1/3 de Simpson é calculado por:

Exemplo: Calcular
usando a regra do
1/3 de Simpson repetida com m = 4.
xi
f(xi)
ci
Verificando
1,0
9,00
1
1,5
22,75
4
2,0
47,00
2
2,5
84,75
4
3,0
139,00
1
Exercícios:
1) Calcule as integrais a seguir usando a regra do 1/3 de
Simpson com 4 e 6 intervalos.
a)
b)
c)
d)
2) Dado a tabela:
x
0
f(x)
1
0,2
0,4
0,6
0,8
1,0
1,2408 1,5735 2,0333 2,6965 3,7183
Qual seria o modo mais adequado de calcular I2 usando
esses dados? Faça o calculo.