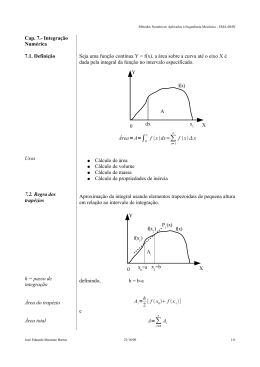
Integração
Numérica
Integral


O conceito de integral esta ligado ao problema de
determinar a área de uma figura plana qualquer.
Integral de uma função f(x) no intervalo [a,b]

A integral da função f(x) é representada por F(x)
F ( x)   f ( x)dx




Em determinados casos, F(x) não pode ser
calculada
Obter F(x) não é trivial.
Nem sempre se tem a forma analítica da função
a ser integrada, f(x), mas uma tabela de pontos
que descreve o comportamento da função
Nestes casos, utilizamos a integração numérica
Integração Numérica

A solução numérica de uma integral é
chamada de quadratura. Há dois
métodos bastante empregados para
calcular a quadratura de uma função que
são chamadas regras de Newton-Cotes:
–
–
Regra dos trapézios
Regra de Simpson
Regra dos trapézios



substituição da função f(x) por um polinômio que a
aproxime no intervalo [a, b] em pontos igualmente
espaçados
O problema fica resolvido pela integração de um
polinômio
Na regra dos trapézios, utiliza-se um polinômio
interpolador de Lagrange do primeiro grau
onde

Integrando no intervalo [a,b] teremos
onde h  x1  x0

O que é a formula da área do trapézio, como
mostrado na figura

Quanto for maior o intervalo, maior será o erro do
método. Dessa forma, um melhoramento no método
consiste em dividir o intervalo em vários pedaços,
calcular a área de cada um deles e em seguida somar
todos
n 1
h
 f ( xi )  f ( xi 1 )
i 0 2
h
h
h
I  ( f ( x0 )  f ( x1 ))  ( f ( x1 )  f ( x2 ))  ...  ( f ( xn 1 )  f ( xn ))
2
2
2
h
I   f ( x0 )  2 f ( x1 )  2 f ( x2 )  ...  2 f ( xn 1 )  f ( xn )
2
I 

Ex:Calcule a integral de f ( x)  e x no intervalo
[0,1] com 10 subintervalos
ba
 0,1
10
h
I  ( f (0)  2 f (0,1)  ...  2 f (0,9)  f (1))
2
h 0
I  (e  2e0,1  ...  2e0,9  e1 )
2
I  1,72
h
Regra 1/3 de Simpson
podemos usar a fórmula de Lagrange para
estabelecer a fórmula de integração
resultante da aproximação de f(x) por um
polinômio interpolador de grau 2
 Seja p2(x) que interpola f(x) nos pontos:
 x0 = a
 x 1 = x0 + h
x2 = x0 + 2h = b

Regra 1/3 de Simpson
p2 ( x ) 
x  x1 x  x2  f ( x )  x  x0 x  x2  f ( x )  x  x0 x  x1  f ( x )
x0  x1 x0  x2  0 x1  x0 x1  x2  1 x2  x0 x2  x1  2
p2 ( x ) 
x  x1 x  x2  f ( x )  x  x0 x  x2  f ( x )  x  x0 x  x1  f ( x )
0
1
2
 h  2h
h  h 
2hh
Resolvendo L0
x2

x0
( X  x1 )( X  x2 ) ( X  x1 )( X  x2 )
1


( x0  x1 )(x0  x2 )
(h)(2h)
2h 2
x2
 ( X  x1 )(X  x2 )
x0
Substituindo (x-x0)/h=y temos que dx = hdy. Daí, temos:
X-x1 =x0+yh-(x0+h)=(y-1)h
X-x2= x0+yh-(x0+2h)=(y-2)h
X=x0->y=0 e X=x2->y=2
2
1
2h
2
 ( y  1)h( y  2)hhdy
0
2
h 2
y  3 y  2dy
2

0
h2 h

23 3
h
w0 
3
x2

x0
4h
w1 
3
w2 
h
3
h
f ( x)dx  [ f ( x0 )  4 f ( x1 )  f ( x 2 )]
3
Exemplo

Estimar o valor da integral de ex no
intervalo [0,1] através da regra 1/3 de
Simpson
Regra 1/3 de Simpson Repetida
b
xm
m 2
x0
k 1
 f ( x )dx   f ( x )dx   
a
x2 k
x2 k  2
f ( x )dx 
h
 f ( x0 )  4f ( x1 )  f ( x2 )  f ( x2 )  4f ( x3 )  f ( x 4 )   
3
 f ( xm 2 )  4f ( xm 1 )  f ( xm )
Exercício

Estimar a integral de e^x no intervalo de
zero a um usando a regra 1/3 de Simpson
repetida 3 vezes