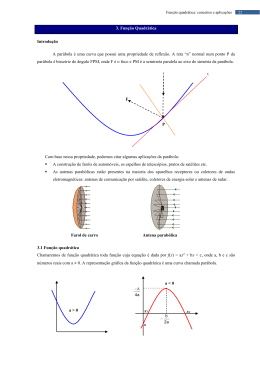
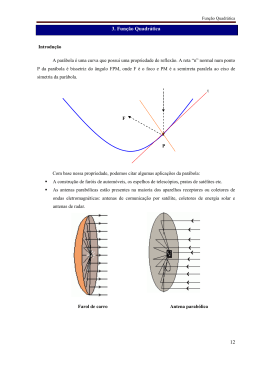
AULA 3
• Função Quadrática
• Função Modular
FUNÇÃO QUADRÁTICA
EXEMPLO
Escreva as seguintes funções na forma fatorada:
f(x) = x2 + 6x + 8
f(x) = - x2 + 4x - 3
f(x) = - 5x2 + 5
Duas raízes reais e diferentes (o gráfico toca o eixo x em
dois pontos )
Duas raízes reais e iguais (o gráfico toca o eixo x em apenas
um ponto)
Nenhuma raiz real (o gráfico não corta o eixo x)
Coordenadas do Vértice da Parábola
Estudo do Sinal da Parábola
EXEMPLOS
1 – Encontre a lei de formação da função quadrática dada abaixo:
Outra maneira...
2 – Uma empresa vendia mensalmente 200 unidades de um
produto a R$ 80,00 cada. Observou-se que, para cada real de
desconto no preço de uma peça, eram vendidas 10 peças a
mais. Calcule o maior faturamento possível.
3 – Faça o gráfico das seguintes funções:
f(x) = x2 - 4x + 5
f(x) = 9 - x2
4 – Para construir um cercado em forma de um retângulo,
Frederico tinha recursos financeiros para fazer apenas 80m
de cerca e resolveu aproveitar uma parte reta de um muro
para economizar e contruiu, com três lances de cerca, um
cercado retangular de área máxima. Qual a área desse
cercado?
Inequações
EXEMPLO
Sistema de Inequações
Inequação Produto
Inequação Quociente
Equações Biquadradas
f(x) = ax4 + bx2 + c
Para resolver basta fazer:
x2 = y
EXEMPLO: Resolver a equação x4 - 10x2 + 9
Função Modular
f(x) = - x, se x < 0
f(x) = |x|
f(x) = x, se x ≥ 0
Im (f) = R+
EXEMPLO
1 – Resolva as equações/inequações modulares:
a) |x – 2| = 6
b) |x – 1| + | x + 6| = 13
c) |4x - 3| > 5 (|x| > a <-> x < -a ou x > a)
d) |3x – 12| + |5 – x| < 12
Propriedades do Módulo
1) a2 = | x|
2) |xy| = |x| . |y|
3) - |x| ≤ x ≤ |x|
4) |x + y| ≤ |x| + |y| (Desigualdade Triangular)
5) |x + y| ≥ |x| - |y|
6) |x – y| ≥ |x| - |y|
EXEMPLO
Esboçar o gráfico da função f(x) = | x2 - 4x + 3|
Exercícios
1 – Em um jogo de futebol, o jogador cobrará uma falta com
barreira. A trajetória da bola, que deve passar sobre a
barreira, descreve aproximadamente o gráfico de uma
parábola. Supondo que h é a altura da bola em relação ao
chão, em metros; t o tempo em segundos após o chute do
jogador; e a parábola descrita pela bola é dada por
h = -t2 + 4t, determine:
a) Em quantos segundos a bola atinge a altura máxima;
b) A altura máxima atingida pela bola.
2 – Quantos números inteiros satisfazem simultaneamente as
desigualdades
x + 3 ≤ 2x + 5 e 4x + 1 ≤ 2x + 3?
3 – Um retângulo tem 40m de perímetro. Determine as
dimensões desse retângulo para que este possua a maior área
possível. Determine a medida dessa área.
4 – Planeja-se construir duas estradas em uma região plana.
Colocando coordenadas cartesianas na região, as estradas
ficam representadas pelas partes do gráfico da parábola
y = - x2 + 10x e da reta y = 4x + 5, com 2 ≤ x ≤ 8. Qual a soma
das coordenadas do ponto representado pela intersecção das
estradas?
EXERCÍCIOS SELECIONADOS
GRUPO 1
1, 4, 5, 7, 8, 9, 11, 12,13, 14, 16, 18, 19, 21, 24, 27, 29, 30 e
31.
GRUPO 2
1, 2, 4, 8, 9, 14, 15, 16, 18, 19, 29, 30, 33, 34 e 38.