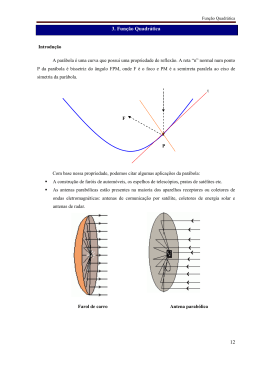
Função quadrática: conceitos e aplicações
3. Função Quadrática
Introdução
A parábola é uma curva que possui uma propriedade de reflexão. A reta “n” normal num ponto P da
parábola é bissetriz do ângulo FPM, onde F é o foco e PM é a semirreta paralela ao eixo de simetria da parábola.
t
F
P
Com base nessa propriedade, podemos citar algumas aplicações da parábola:

A construção de faróis de automóveis, os espelhos de telescópios, pratos de satélites etc.

As antenas parabólicas estão presentes na maioria dos aparelhos receptores ou coletores de ondas
eletromagnéticas: antenas de comunicação por satélite, coletores de energia solar e antenas de radar.
Farol de carro
Antena parabólica
3.1 Função quadrática
Chamaremos de função quadrática toda função cuja equação é dada por f(x) = ax2 + bx + c, onde a, b e c são
números reais com a  0. A representação gráfica da função quadrática é uma curva chamada parábola.
a<0

4a
a>0
x1
c
x2
b

2a
22
Função quadrática: conceitos e aplicações
3. 2 Pontos notáveis para construção do gráfico de uma parábola
Vamos agora determinar alguns pontos que são importantes para a construção do gráfico de uma parábola.
a) ponto onde a parábola intercepta o eixo y
Como no eixo y temos x = 0, substituindo na equação da parábola encontramos y = c.
b) pontos onde a parábola intercepta o eixo x
Como no eixo x temos y = 0, teremos ax2 + bx + c = 0  x =
b 
onde  = b2 – 4ac.
2a
Resolvendo a equação do 2° grau encontraremos as raízes da função: x1 e x2
c) vértice da parábola :
xv =
x  x2

b
e yv =
ou então temos: xv = 1
e yv = f(xv)
2
4a
2a
Exemplo: Utilizando os pontos notáveis, esboce o gráfico das funções abaixo:
a)
y = x2 – 6x + 5
b) y = - x2 + 4
c)
p = t2 + 1
d) S = t2 – 4t + 4
3.3 Aplicações
Problema 1. Uma bola é atirada para cima, do alto de um rochedo de 160 pés de altura. A velocidade inicial
(componente vertical) da bola é de 48 pés/s. Sabendo que a altura S da bola, em cada instante t, é dada pela função
horária S = So + vot +
1 2
gt onde g = 32 pés/s2 (aceleração da gravidade) determine:
2
a) A equação horária do movimento vertical dessa bola.
b) A altura da bola 3s após o lançamento.
c) O tempo que a bola leva para atingir o solo.
d) A altura máxima alcançada pela bola.
23
Função quadrática: conceitos e aplicações
Problema 2. Com uma folha de zinco de 60 cm de largura, pretende-se construir uma calha de secção transversal
retangular conforme a figura abaixo:
a) Determine a área da secção em função de x e o gráfico dessa função.
b) Encontre o valor de x para que a vazão da calha seja máxima.
Problema 3. Os cabos da ponte pênsil, indicada na figura abaixo, tomam a forma de arcos de parábola. As torres
de suporte têm 24 metros de altura e há um intervalo entre elas de 200 metros. O ponto mais baixo de cada cabo
fica a 4 metros do leito da estrada. Considerando o plano horizontal do tabuleiro da ponte contendo o eixo dos x e
o eixo de simetria da parábola como sendo o eixo dos y, perpendicular a x, determine o comprimento do elemento
de sustentação AB, que liga verticalmente o cabo parabólico ao tabuleiro da ponte, situado a 50 m do eixo y.
Problema 4. A corrente que circula por um resistor de 20  varia com o tempo de acordo com o gráfico abaixo:
Sabendo-se que potência elétrica instantânea (P) absorvida pelo resistor em função do tempo é dada por P = Ri2,
encontre a equação de P = f(t) para 2 ≤ t ≤ 6 e esboce seu gráfico.
24