O que é o Cabri-Géomètre?
O Cabri-Géomètre é um software que permite
construir todas as figuras da geometria elementar
que podem ser traçadas com a ajuda de uma régua
e de um compasso. Uma vez construídas, as figuras
podem se movimentar conservando as propriedades
que lhes haviam sido atribuídas. Essa possibilidade
de deformação permite o acesso rápido e contínuo a
todos os casos, constituindo-se numa ferramenta
rica de validação experimental de fatos
geométricos. Ele tem outros aspectos que vão muito
além da manipulação dinâmica e imediata das
figuras.
O Cabri está disponível em mais de 40 países e em 24
idiomas diferentes. Ele é uma ferramenta auxiliar no
ensino-aprendizagem da Geometria e é utilizado no:
•Ensino Médio
•Ensino Fundamental
•Ensino Superior
Características do Cabri-géomètre
•Geometria Dinâmica
- Figura com movimento mantendo as suas propriedades
•Construtivista
- O aluno cria as suas atividades construindo seu
conhecimento
•Software Aberto
- O professor cria as atividades como queira
•Trabalhar Conceitos
- Construções de figuras geométricas
•Explorar Propriedades dos Objetos e suas Relações
- Comprovar Experimentalmente
•Construção de Figuras Geométricas
•Formulação de Hipóteses e Conjecturas
•Históricos das Construções
•Criação de Macros
O Cabri permite ao professor criar livremente atividades
para suas aulas, ele é assim caracterizado como um
software aberto. Ele pode ser utilizado desde o primário até
a Universidade em diversas áreas como Matemática, Física
e Desenho Artístico por exemplo.
O Cabri-Géomètre é um software desenvolvido por J. M.
Laborde, Franck Bellemain e Y. Baulac, no Laboratório de
Estruturas Discretas e de Didática da Universidade de
Grenoble. Este é um laboratório associado ao CNRS,
instituição francesa equivalente ao CNPq brasileiro.
O Cabri-Géomètre é representado no BRASIL desde 1992
pela PROEM na PUC-SP.
Neste projeto, tem-se como objetivo mostrar uma
aplicação do Teorema de Pitágoras, bem como, uma
aplicação da trigonometria como forma alternativa para
resolução de problemas no triângulo retângulo.
O problema foi esquematizado por meio do
programa Cabri-Geometré, que como já foi dito que nos
fornece um ferramental bastante interessante, para o
ensino direto da Geometria. Porém, com a devida
contextualização, os problemas podem englobar vários
tópicos matemáticos.
PROBLEMA: Como podemos observar na figura
abaixo, o planeta Katatum, da Galáxia de Nióbio, possui dois
satélites naturais em sua órbita.
Sabe-se que o raio do planeta Katatum é 25 mil
quilômetros e que o raio dos satélites está alinhado conforme
a figura. Além disso, sabe-se que os satélites estão deslocados
horizontalmente, formando um ângulo de 30o. Qual a
distância entre os satélites? Qual o comprimento do
segmento que vai de B à C?
Lembre-se: A distância entre dois planetas é a medida
entre seus raios.
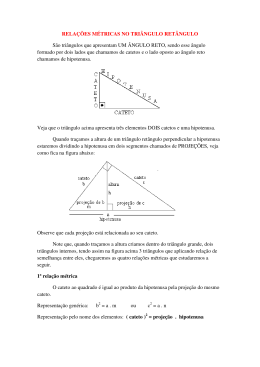
Em primeiro lugar, deve-se discutir a geometria do
problema. Como pode-se observar, as retas que contém os
pontos K e C é paralela à reta que contém os pontos T e A.
Como essas retas paralelas são paralelas, por
transporte de segmentos a medida do diâmetro do planeta
Katatum é igual à medida do segmento que vai do ponto C ao
ponto A. Lembrando que o raio do planeta é 25 000 Km, temos
que medida de CA é igual à 50 000 Km.
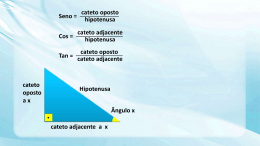
Fazendo uma aplicação trigonométrica, pois o triângulo
ABC é retângulo, temos:
cos 30º = cateto adjacente / hipotenusa
[3(1/2)] / 2 = 50 000 / hipotenusa
hipotenusa = [100 000 . 3(1/2) ]/ 3
Nesse ponto, temos duas alternativas:
I.
Achar o terceiro segmento através da
trigonometria, como anteriormente.
II. Achar o terceiro segmento pelo Teorema de
Pitágoras.
I. sen 30º = cateto oposto / hipotenusa
0,5 = cateto oposto / {[100 000 . 3(1/2) ]/ 3}
Fazendo as devidas operações obtemos:
cateto oposto = [ 50 000 . 3(1/2) ] / 3
II. (hipotenusa)2 = (cateto BC)2 + (cateto CA)2
{ [100 000 . 3(1/2) ] / 3 } 2 = (cateto BC)2 + 50 000 2
(100 000 2 . 3 / 9) - 50 000 2 = (cateto BC)2
(cateto BC)2 = (100 000 2 / 3) - 50 000 2
E fazendo as devidas operações, temos:
(cateto BC)2 = (25 . 100 000 2 / 3)
cateto BC = [ 50 000 . 3(1/2) ] / 3
Como podemos observar, obtivemos o resultado
obtido em I.
Podemos, portanto, responder às questões:
A distância entre os satélites é igual a [100 000 . 3(1/2) ]/ 3
e o comprimento do segmento BC é [ 50 000 . 3(1/2) ] / 3 .