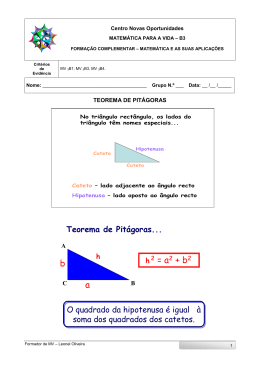
Relações métricas no triângulo
retângulo
Hipotenusa e catetos do
triângulo retângulo
Catetos: são os dois lados que formam o ângulo reto.
Hipotenusa: é o lado oposto ao ângulo reto.
cateto
hipotenusa
cateto
cateto
hipotenusa
cateto
Outros segmentos do triângulo
retângulo
a: é a hipotenusa.
b e c: são os catetos
h: é a altura do triângulo em relação à hipotenusa.
m: é a projeção do cateto b sobre a hipotenusa.
n: é a projeção do cateto c sobre a hipotenusa.
c
b
h
n
m
a
A altura h divide o triângulo ABC em dois triângulos
retângulos, ABH e ACH.
A
h
B
H
C
Os triângulos ABC, ABH e ACH são
semelhantes. Veja:
A
(I)
 +  = 90º
 
h

B

H
C
(I)
 +  = 90º
(II)
 +  + 90º = 180º
 +  = 90º
 


Comparando (I) e (II), tem-se:
 +  =  +    = .
Portanto,  = .
(I)
 +  = 90º
(III)
 +  + 90º = 180º
 +  = 90º
 

Comparando (I) e (III), tem-se:
 +  =  +    = .
Portanto,  = .

A
Conclusão


h

B

Como  =  e  = ,
os triângulos ABC,
ABH e ACH são
semelhantes pelo
caso (AA).
C
H
A
A
A




B
H
B


C H
C
1ª relação métrica
A
A
b
c
h
h
m
n
B
H
H
h m

n h
2
h  mn
C
2ª relação métrica
A
A
b
b
c
h
m
B
a
C
H
b m

a b
b2  m  a
C
3ª relação métrica
A
c
A
b
c
h
n
B
h
H
n
B
n c

c a
a
C
b
c
c2  n  a
c
a
4ª relação métrica
A
c
A
b
c
h
n
B
h
H
n
c
B
h b

c a
ah  bc
a
C
b
c
a
Teorema de Pitágoras
(5ª relação métrica)
Somando, membro
a membro, as duas
igualdades, tem-se:
c
b
h
b2  m  a
c2  n  a
n
m
a
2ª relação: b² = m . a
3ª relação: c² = n . a
Observe que a = m + n
b2  c 2  m  a  n  a
b2  c 2  am  n
b2  c 2  a  a
b2  c 2  a2
Teorema de Pitágoras
Em um triângulo retângulo, o quadrado da hipotenusa
é igual à soma dos quadrados dos catetos.
A
B
a² = b² + c²
b
c
a
C
Resumo
Relações métricas:
1ª) h² = m . n
c
b
h
2ª) b² = m . a
3ª) c² = n
.a
m
n
a
4ª) a . h = b . c
Teorema de Pitágoras
5ª) a² = b² + c²