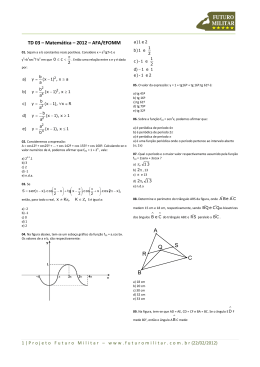
▼
Questão 22
—
No losango ABCD de lado 1, representado na figura, tem-se que M é o ponto médio de AB , N é o ponto médio
—

de BC e MN = 14 . Então, DM é igual a
4

D
C
a) 2
4

b) 2
2
N
2
c) 

d) 3 2
A
B
M
2

5
2
e)
2
Resolução
Do enunciado, temos a figura:
D
1
A
14
α
1
2
C
M
4
α 1
º–
0
2
18
B
1
2
N
1
2
0°  α  180°
Aplicando o teorema dos cossenos no triângulo MBN, temos:
14 2 1 2 + 1 2 – 2 ⋅ 1 ⋅ 1 ⋅ cos (180° – α)
=
2
2
2 2
4
14 = 1 + 1 – 1 ⋅ cos (180° – α)
16 4 4 2
1 ⋅ cos (180° – α) = 2 – 14
2
4 16
( ) () ()
1 ⋅ cos (180° – α) = – 6 ∴
2
16
cos (180° – α) = – 3 e cos α = 3 (I)
4
4
Aplicando o teorema dos cossenos no triângulo DMA, temos:
2
(DM)2 = 12 + 1 – 2 ⋅ 1 ⋅ 1 ⋅ cos α (II)
2
2
()
De (I) e (II), resulta que
(DM)2 = 1 + 1 – 2 ⋅ 1 ⋅ 1 ⋅ 3
4
2 4
2

(DM)2 =
∴ DM = 2
4
2
Resposta: b