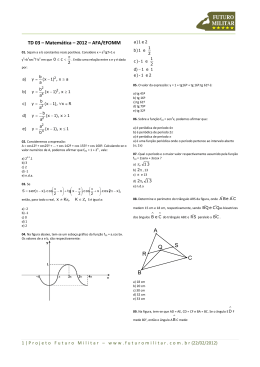
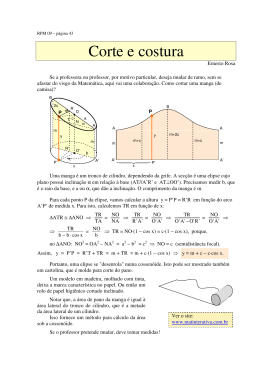
Sn= (a1 + an).n/2 e an= a1 + (n – 1).r NOTE QUE Sn = 16.500 Os valores doados constituem uma progressão aritmética de primeiro termo igual a 350 e razão 50. Logo, se n é o número de microempresas que participaram da campanha, então n 1 50 16500 350 n 2 n 20 n 2 13n 660 0 Resposta da questão 2: [D] 1 2 V(t) t 3 43200 1 0 t2 3 43200 t 2 129600 t 360min t 6h Resposta da questão 3: [B] Devemos considerar a retirada de 3 bolinhas de 300 g para que a massa total seja 900g. Portanto, a probabilidade P pedida é: 7 6 5 7 2 5 7 P . 10 9 8 10 3 8 24 Resposta da questão 4: [D] Supondo que todos aparecerão na foto lado a lado, temos 2 possibilidades para os avós e P8 8! 40320 possibilidades para os netos. Portanto, pelo Princípio Fundamental da Contagem, existem 2x40.320 = 80.640 maneiras distintas de fazer a foto. Resposta da questão 5: [D] Considere a figura. l 8 l 2 É fácil ver que os triângulos BFE e DGC são semelhantes por AA. Portanto, se é a medida do lado do quadrado, temos. 2 8 2 16 4. Resposta da questão 6: [E] Seja V o volume real do armário. O volume do armário, no projeto é 3 x 2 x 1 = 6cm³ Logo temos 3 6 1 3 V 6.000.000cm . V 100 Resposta da questão7: [E] Se x é agudo, então cosx > 0. Logo, temos 1 2 cos x 2 tg x 1 2 cos x 1 2 3 1 10 cos x . 10 Resposta da questão 8: [C] Sabendo que y 2,08 x tem-se que o resultado pedido é igual a (VF – VI)/ VI. 100% 2,08 x x 100% 108,0%. x
Baixar