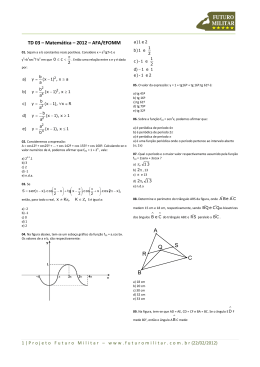
MINISTÉRIO DA DEFESA NACIONAL
FORÇA AÉREA
COMANDO DE PESSOAL
CENTRO DE FORMAÇÃO MILITAR E TÉCNICA DA FORÇA AÉREA
CONCURSO DE ADMISSÃO AO CFS/QP 2011 / 2012
PROVA DE MATEMÁTICA
ABRIL DE 2011
LEIA ATENTAMENTE AS SEGUINTES INSTRUÇÕES
1. Na sua folha de respostas, preencha a sua identificação somente no destacável. O
não comprimento deste ponto implica a anulação da prova;
2. O tempo total da prova é de 90 minutos, com 15 minutos de tolerância;
3. Leia cuidadosamente o texto e certifique-se que percebeu a pergunta antes de
responder;
4. Se tiver dificuldade em responder a qualquer questão, passe adiante e tente
resolvê-la posteriormente;
5. Após a conclusão da sua prova, deixe sobre a carteira este enunciado e as folhas
de resposta.
Tenha calma e ... BOM TRABALHO
Prova de Matemática CFS/QP – 2011 / 2012
ABR11
1ª Parte
Os dez itens deste grupo são de escolha múltipla.
Para cada item, são indicadas quatro alternativas, das quais só uma está correcta.
Escreva na sua folha de respostas apenas a letra correspondente à alternativa que considera
estar correcta.
Se apresentar mais do que uma letra, a classificação será de zero pontos, o mesmo
acontecendo se a letra transcrita for ilegível.
Não apresente cálculos, nem justificações.
1. O valor numérico da expressão
4
(A)  
6
2. A expressão
6
(
(A) 4 5
1 1

 −1 − + 
6 3

5
 
6
6
(B)  
4
5+2
)2 − 4
−18
−19
, é:
6
3
(C)  
4
6
4
(D)  
3
6
20 − 9 , é equivalente a uma expressão do tipo a b . Qual?
(B) − 7 5
(C) − 4 5
(D) 5 7
3. De um triângulo equilátero sabemos que o lado mede 4.
Podemos afirmar que a sua área mede:
(A)
6
(B) 4 3
(C)
3
(D) 2 6
 3π

π

4. A expressão sen (x − 5π ) + cos  π + x  − sen  − x  , é equivalente a:
 2

2

(A) − cos x
(B) cos x
(C) − tan x
(D) tan x
Página 1 de 6
Prova de Matemática CFS/QP – 2011 / 2012
ABR11
5. Considere uma circunferência de centro C e raio 2, tangente a uma recta s. Um ponto P
começa a deslocar-se sobre a circunferência, no sentido indicado na figura.
s
s
d(x)
C
P
C
P
x
Seja d(x) a distância de P a s, após uma rotação de amplitude x.
Qual das igualdades seguintes é verdadeira para qualquer número real positivo x?
(A)
(B)
(C)
(D)
d ( x ) = 2 + 2 senx
d ( x ) = 2 + 2 cos x
d ( x ) = 2 + cos x
d ( x ) = 2 − 2 cos x
6. Seja h uma função de domínio IR, injectiva e tal que f ( 0 ) = 0 .
Qual das afirmações é verdadeira?
(A) h não tem zeros
(B) h tem exactamente um zero
(C) h tem exactamente dois zeros
(D) h tem mais que dois zeros
7. Um carro deslocou-se segundo uma linha recta, à qual se associou um eixo Ox com
sentido positivo da esquerda para a direita. O carro arrancou da origem do eixo e
aumentou rapidamente de velocidade, estabilizando ao fim de um certo intervalo de
tempo.
Qual dos seguintes gráficos descreve a velocidade do carro, em função do tempo?
Página 2 de 6
Prova de Matemática CFS/QP – 2011 / 2012
ABR11
8. Qual dos seguintes pares ordenados é solução do sistema
8y

 2x −
=6
?

3
1 − ( x − 3 y ) = 0
 23 6 
(A)  − , − 
5
 5
 23 6 
(B)  , 
 5 5
9. As soluções da equação
(A) 0 e
2
 23 6 
(C)  − , 
 5 5
 23 6 
(D)  , − 
5
 5
2 x − x 2 = 0 são:
(B) -1 e
(C) - 2 e
2
(D) -1 e
2
2
10. A solução da equação log ( x + 1 ) − log x = log ( 2 x ) , é:
(A) 0
(B) 1
(C) 2
(D) 3
2ª Parte
Nos itens deste grupo apresente o seu raciocínio de forma clara, indicando todos os cálculos que
tiver de efectuar e todas as justificações necessárias.
Atenção: quando, para um resultado, não é pedida a aproximação, pretende-se sempre o valor
exacto.
1. Efectue e simplifique o mais possível:
(x + 5 )2 = (1 − x ) (1 + x ) + 24
2. Para construir um aeródromo vai-se reservar
um terreno rectangular que tem de conter uma
faixa com 2 hm de largura para a construção
de diversos edifícios.
A restante área (tracejada) tem de ter 10 hm 2 .
2.1. Determine para que valores de x, o
comprimento do aeródromo excede 12 hm.
2.2. Sabendo que se gastaram 40 hm lineares de vedação
para cercar o aeródromo, calcule a sua largura (x).
2 hm
x
10 hm 2
y
Página 3 de 6
Prova de Matemática CFS/QP – 2011 / 2012
ABR11
3. Na figura estão representados os gráficos de duas funções f (afim) e g (quadrática).
8 y
7
6
5
4
3
2
1
0
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1 0
-2
-3
-4
-5
-6
-7
-8
f
x
1
2
3
4
5
6
7
8
9 10
g
Observando os gráficos das funções, indique o conjunto solução de cada uma das condições:
3.1. g ( x ) − f ( x ) ≥ 0
3.2. − g ( x ) − 6 < 0
4. Relativamente à figura junta, sabe-se que:
• o triângulo [ABD] é rectângulo
• o ponto C pertence ao cateto [BD]
• x designa a amplitude, em radianos, do ângulo BAD
• AB = 2 e BC = 1
Mostre que a área do triângulo [ACD], é dada por:
2t g ( x ) − 1
FIM
Página 4 de 6
Prova de Matemática CFS/QP – 2011 / 2012
ABR11
Cotação (em pontos)
1ª Parte .....................................................................................100 pontos
Cada resposta certa...................10 pontos
Cada resposta errada...................0 pontos
Cada resposta não respondida ....0 pontos
2ª Parte ...................................................................................100 pontos
1..............................................................................15 pontos
2..............................................................................35 pontos
2.1………………………………………….15 pontos
2.2……………………………………….…20 pontos
3..............................................................................30 pontos
3.1…………………………………………15 pontos
3.2…………………………………………15 pontos
4..............................................................................20 pontos
Página 5 de 6
Prova de Matemática CFS/QP – 2011 / 2012
ABR11
FORMULÁRIO
Áreas de figuras planas
Diagonal maior × Diagonal menor
Volumes
Pr isma : Área da Base × Altura
Losango :
1
2
Pirâmide :
× Área da Base × Altura
3
Base maior + Base menor
Trapézio :
× Altura
2
1
Círculo : πr
2
Cone :
Base × Altura
Esfera :
× Área da Base × Altura
3
4
Triângulo :
πr
3
3
2
Página 6 de 6