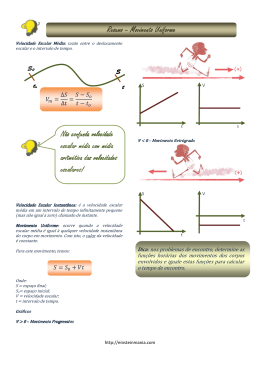
MOVIMENTO
RETILÍNEO UNIFORME
Prof. Emerson
MOVIMENTO RETILÍNEO UNIFORME

Conceito:
Quando o móvel percorre espaços iguais em
tempos iguais, não acontecendo mudanças na
direção e sentido do movimento. Logo neste
movimento a velocidade escalar é constante
em qualquer instante ou intervalo de tempo.
Como no movimento uniforme a velocidade
não se altera, a aceleração é nula (a = 0).
MOVIMENTO RETILÍNEO UNIFORME
Neste exemplo de MRU, em qualquer instante
ou intervalo de tempo a velocidade é sempre
igual a 5m/s.
MOVIMENTO RETILÍNEO UNIFORME
Se a velocidade escalar é constante em
qualquer instante ou intervalo de tempo, a
velocidade escalar média no movimento
uniforme sempre será igual à instantânea:
VELOCIDADE INSTANTÂNEA

Ou simplesmente velocidade, é similar a
velocidade média. A diferença está no fato de que
Δt é tomado como sendo infinitamente pequeno,
isto é, o intervalo de tempo reduz-se a um
instante de tempo. Portanto, pode-se dizer que a
velocidade média torna-se a velocidade naquele
instante.
VELOCIDADE INSTANTÂNEA
Ex: Imagine-se dirigindo um carro, a partir de certo instante você olha
para o velocímetro e para o relógio e começa a anotar as velocidades
indicadas no decorrer do tempo. Suponha que os valores anotados
sejam os da tabela abaixo:
Para cada instante podemos associar um valor para a velocidade do
automóvel. Portanto, para cada valor indicado pelo velocímetro num dado
instante denominamos velocidade escalar instantânea.
UNIDADES DE CONVERSÃO
No Sistema Internacional (SI), a unidade para a velocidade é o metro por
segundo (m/s). Outras unidades, tais como cm/s e km/h, são muito
utilizadas.
As relações entre elas são as seguintes:
Logo, para transformar km/h em m/s, dividimos por 3,6 e para o inverso,
multiplicamos por 3,6.
Como exemplo, suponha um carro efetuando um deslocamento escalar de 36
km num intervalo de tempo de 0,50 h. A sua velocidade escalar média neste
percurso corresponde a:
FUNÇÃO HORÁRIA DO MOVIMENTO UNIFORME
Também conhecida como:
Essa expressão é denominada função horária do movimento uniforme. Com ela
podemos localizar, em qualquer instante, um móvel que se movimenta em
velocidade constante, desde que saibamos seu espaço inicial e sua velocidade.
TIPOS DE MOVIMENTOS
MOVIMENTO RETRÓGRADO ← é quando um móvel se movimenta no
sentido contrário ao do positivo da trajetória.
MOVIMENTO PROGRESSIVO → é quando um móvel se movimenta no
sentido positivo da trajetória.
EXERCÍCIO DE FIXAÇÃO
4) Dada a função horária S = 10 + 3t, válida no SI. Determine:
a) O espaço inicial, a velocidade escalar e o sentido do movimento
em relação à trajetória;
b) O espaço em 5s
c) O instante em que s = 31m
Resolução:
a) S0 = 10m, v = 3m/s. O movimento é
progressivo, pois a velocidade escalar é
positiva.
b) S = 10 + 3(5) = 10 + 15 = 25m
c) 31 = 10 + 3t ⇒ 3t = 21 ⇒ t = 7s
GRÁFICOS

A utilização de gráficos é uma poderosa arma para
interpretação de dados, mostrando a evolução no tempo de
grandezas como espaço e velocidade .
a) Posição (s) x Tempo (t)
EXERCÍCIO DE FIXAÇÃO
5) Com base no gráfico, referente ao movimento de um móvel,
podemos afirmar que:
a) A função horária do movimento é S = 40 + 4 t;
b) O móvel tem velocidade nula em t = 20s;
c) O móvel passa pela origem em 20s;
d) A velocidade é constante e vale 4m/s;
e) O móvel inverte o sentido do movimento no instante t = 10s.
Resposta correta: d)
80  (40)
V
 4m / s
30  0
GRÁFICOS
Velocidade x Tempo
Como no movimento uniforme a velocidade linear é constante positiva
ou negativa.
EXERCÍCIO DE FIXAÇÃO
6) Dada a tabela abaixo encontre:
a) A função horária
b) Gráficos s x t e v x t
EXERCÍCIO DE FIXAÇÃO
7) Dois carros A e B movimentam-se na mesma rodovia. No instante t = 0,
suas posições e os respectivos módulos de suas velocidades escalares
constantes estão indicadas na figura abaixo. Determine o ponto de
encontro dos automóveis.
Resolução:
As funções horárias dos carros A e B são: SA = 20 + 60t e SB = 300 – 80t
No ponto de encontro temos SA = SB então: 20 + 60t = 300 – 80t ⇒ t = 2h
Substituindo t = 2h nas equações horárias dos dois carros:
SA = 20 + 60.(2) ⇒ SA = 140 km e
SB = 300 – 80.(2) ⇒ SB = 140 km
Portanto, o encontro dos carros A e B ocorre no
km 140, ou seja, a 140 km da origem dos espaços.
Construindo-se os gráficos s x t para os dois móveis,
percebe-se o processo de encontro ocorrido.