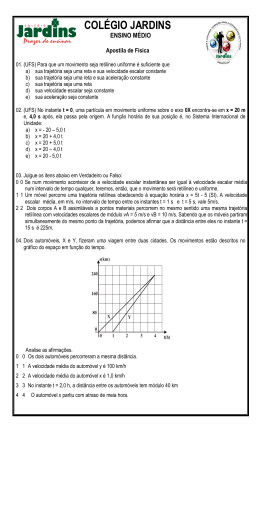
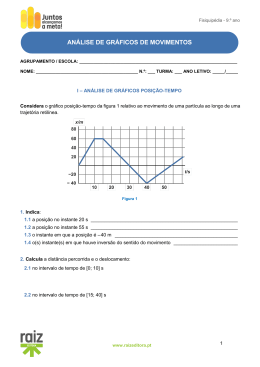
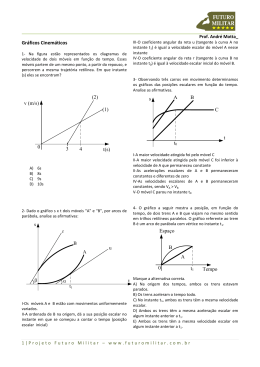
1 – Um trem de comprimento L atravessa um túnel reto de comprimento 220 m, com movimento
uniformemente variado. Quando o trem começa a entrar no túnel, sua velocidade escalar é de 12 m/s
e, quando acaba de sair do túnel, sua velocidade escalar é de 18 m/s. Sabendo que a travessia levou
20s, determine:
( 0,5 ) a) a aceleração escalar do trem.
( 0,5 ) b) o valor de L.
2 – Um carro viaja com velocidade de 72 km/h em um trecho retilíneo de uma rodovia. Subitamente, o
motorista vê um carro parado na pista. Entre o instante em que o motorista avista o animal e aquele
em que começa a frear, o carro percorre 10 m. O motorista freia o carro à taxa constante de 5 m/s2,
mantendo-o em sua trajetória retilínea e consegue parar antes de atingir o cavalo, que permaneceu
imóvel durante todo o tempo.
(0,5) a) A que distância mínima do animal o motorista deve tê-lo avistado?
(0,5) b) Construa o gráfico da velocidade escalar em função do tempo desde o instante em que ele
avista o animal até o instante em que o carro para.
3 - Uma partícula movimenta-se numa trajetória retilínea
e sua velocidade escalar varia com o tempo conforme o
gráfico a seguir. Considere que o espaço inicial da
partícula tenha sido a origem dos espaços.
Analise as afirmações abaixo a respeito desse movimento
e classifique cada uma delas em verdadeira (V) ou falsa
(F).
(
(
(
(
) Houve apenas uma inversão de sentido e ocorreu no instante 5s.
) A partícula passa pela posição 28 m duas vezes nesse intervalo de tempo representado. A
primeira vez no instante 5 s e pela segunda vez no instante 9s.
) A aceleração da partícula entre os instantes 5 e 9 segundos foi constante e seu valor em
módulo é 4 m/s2.
8
)
A equação horária dos espaços para os três primeiros segundos é: 𝑠 = . 𝑡 2 (𝑆𝐼)
3
(
) A distância total percorrida no intervalo de 0 a 9s foi de 44 m.
4 – Partindo da origem do sistema cartesiano, uma partícula realiza 5 deslocamentos sucessivos
representados pelos vetores:
⃗⃗⃗⃗
𝑑1 = 1𝑥 + 3𝑦 ; ⃗⃗⃗⃗
𝑑2 = 3𝑥 + 1𝑦 ; ⃗⃗⃗⃗
𝑑3 = 3𝑥 ; ⃗⃗⃗⃗
𝑑4 = −2𝑦 ;
⃗⃗⃗⃗
𝑑5 = −3𝑥 + 1𝑦
onde 𝑥 𝑒 𝑦 são os versores
representados. Sabendo que a partícula levou um tempo
de 4s para realizar os cinco deslocamentos e considerando
√10 = 3,16, pede-se:
(0,4) a) represente no gráfico acima os deslocamentos
realizados pela partícula.
(0,3) a) determinar o módulo da velocidade escalar média
da partícula.
(0,3) b) determinar o módulo da velocidade vetorial média
da partícula.
5 – Um corpo é lançado verticalmente para cima a 25 m de altura em relação ao solo com uma
velocidade de 20 m/s no instante t0 = 0. Desprezando a resistência do ar e considerando g = 10 m/s2,
pedem-se:
(0,3) a) o instante em que o corpo atinge a altura máxima.
(0,2) b) a equação horária dos espaços adotando o solo como origem dos espaços.
______________________________________
(0,2) c) o instante em que o corpo atinge o solo.
(0,3) d) a altura máxima atingida pelo corpo em relação ao solo.
6 – Numa experiência, certa quantidade de gás ideal ocupa um volume de 25 litros, exerce sobre as
paredes do reservatório uma pressão de 2 atm e se encontra numa temperatura de 32°C.
Considerando-se a constante universal dos gases 0,082 (atm.L)/(mol.K), pode-se afirmar que o número
de mols dessa amostra de gás é de, aproximadamente:
a) 0,5
b) 2
c) 3,5
d) 21
e) 45
7 – Um mol de gás ideal sofre a transformação A → B → C indicada no diagrama pressão x volume da
figura.
Dados: R = 0,082 atm.L/mol.K ; 1 atm = 1.105 Pa ; 1 L = 10-3 m3
(0,4) a) Qual é a temperatura do gás no estado A?
(0,4) b) Qual é o trabalho realizado pelo gás na expansão A →
B? Dê a resposta em joules.
(0,3) c) Qual foi a quantidade de calor recebida pelo gás na
transformação A → B → C ?
8 – Em um recipiente termicamente isolado e de capacidade térmica desprezível, são colocados 2,0
litros de água. Um resistor R = 1,8 Ω é imerso na água e conectado, durante 5 minutos, diretamente a
uma bateria de 12 V e de resistência interna nula (veja a figura).
Dados:
- calor específico sensível da água: c = 1,0 cal/g°C
- 1 cal = 4 J
- densidade da água : d = 1,0 kg/L
Determine para esse intervalo de 5 minutos:
a) a energia dissipada pela resistência.
b) a elevação de temperatura da água considerando que toda a
energia dissipada pela resistência é absorvida pela água.
9 – No circuito abaixo, a corrente na resistência de 10 Ω é nula e a potência dissipada na resistência de
2 Ω é de 18 W.
Determine:
a) a corrente total que atravessa a bateria (i).
b) a força eletromotriz da bateria (E).
10 – A figura mostra o esquema de ligação de um aquecedor elétrico construído com quatro resistores
ôhmicos iguais de resistência R. Os fios e a chave CH têm resistências desprezíveis. A chave pode ser
ligada no ponto 1 ou no ponto 2 e o aparelho é sempre ligado a uma diferença de potencial constante
U. Quando a chave CH é ligada no ponto 1, o amperímetro ideal mostrado na figura indica uma
corrente de intensidade 3,0 A e os resistores dissipam, no total, 360 W.
a) o valor de U.
b) o valor de R.
c) o gasto mensal em reais pela energia consumida se o
aquecedor ficar na posição 2 por duas horas diárias
considerando que 1 kWh custa R$ 0,50.