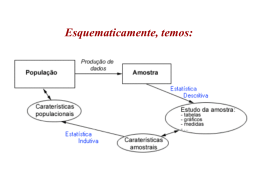
POPULAÇÃO
População Estatística: é o conjunto
de entes portadores de pelo menos
uma característica comum.
Ex: Os estudantes, constituem uma
população, pois apresentam uma
característica comum: são os que
estudam.
AMOSTRA
A amostra é um subconjunto da população,
ou seja, é um conjunto de elementos
extraídos da população.
AMOSTRAGEM
Amostragem é uma técnica para recolher
amostras, garantindo que cada elemento da
população tenha a mesma chance de ser
escolhido.
VANTAGENS: Economia; Tempo; Confiabilidade dos
dados e Operacionalidade.
NÃO SE USA
AMOSTRAGEM
• População muito pequena.
• Necessidade de alta Precisão.
Amostragem casual ou aleatória
simples – pode ser realizada
numerando-se a população de 1 a n e
sorteando-se, a seguir, por meio de um
dispositivo aleatório qualquer.
Podemos exemplificar através do
sorteio lotérico.
Amostragem sistemática –
(quando os elementos estão
ordenados) Consiste em selecionar um
ponto de partida aleatório e, em
seguida tomar cada “n” elementos de
uma lista.
, Onde N é a população e
n é o tamanho da amostra.
Ex: Temos uma lista de 5000 nomes e queremos
selecionar uma amostra de 100 pessoas.
=
= 50
O intervalo entre os nossos selecionados será 50.
1º - Selecionamos um número de 1 a 50, (Ex:23).
2º - O nosso primeiro entrevistado será o nº 23, o
segundo o nº 73
3º - Assim forma-se a sequência de entrevistados
até formar as 100 pessoas.
Amostragem proporcional
estratificada – Como é provável que a
variável em estudo apresente, de estrato em
estrato, um comportamento heterogêneo e,
dentro de cada estrato, um comportamento
homogêneo, convém que o sorteio dos
elementos da amostra leve em
consideração tais estratos. Ou seja,
consideramos a existência dos estratos,
obtendo os elementos da amostra
proporcional ao número de elementos dos
mesmos
Amostragem estratificada uniforme
Não utiliza o critério de
proporcionalidade, pois se seleciona a
mesma quantidade de elementos de
cada extrato.
Tamanho mínimo de uma
amostra aleatória
estratificada proporcional
• 1º Processo: cálculo da amostra Ideal:
• 2º Processo: cálculo da Amostra mínima:
• 3º Processo: cálculo do Estimador de
Amostra:
• 4º Processo: Aplicação do Estimador aos
Estratos = Estrato x Estimador.
Sendo:
N = Tamanho da População;
n = Tamanho da Amostra;
n0 = Tamanho da Amostra Ideal;
E0 = Erro Amostral Tolerável.
Ex:Utilizando a tabela a
seguir, qual deve ser o
tamanho mínimo de uma
amostra aleatória simples, por
curso, tal que possamos
admitir, com alta confiança,
que os erros amostrais não
ultrapassem 5 %?
CURSO
CEX
CON
DIR
FIN
INF
MDA
MKT
ENG
REH
TUR
TOTAL
ALUNOS
870
662
1555
245
529
340
2423
370
577
945
8516
AMOSTRA
TABELAS
São utilizadas para organizar,
facilitar a visualização e comparação
dos dados.
Partes Fundamentais: Título,
cabeçalhos, dados e rodapé (fonte).
SÉRIES ESTATÍSTICAS
Denominamos série estatística
toda tabela que apresenta a
distribuição de um conjunto de
dados estatísticos em função da
época, do local ou da espécie.
As séries estatísticas podem ser:
histórica, geográfica e específica.
SÉRIES TEMPORAIS,
CRONOLÓGICAS, HISTÓRICAS,
EVOLUTIVAS.
Apenas o Tempo varia,
permanecendo constante o fato e
o local.
SÉRIE TEMPORAL
SÉRIES GEOGRÁFICAS, ESPACIAIS,
TERRITORIAIS OU DE LOCALIZAÇÃO.
Apenas o local (fator geográfico)
varia, permanecendo constante o
fato e o tempo.
SÉRIE GEOGRÁFICA
SÉRIES ESPECÍFICAS OU
CATEGÓRICAS
Apenas o fato varia, enquanto o
tempo e o local não se altera.
Predomina a discriminação
segundo categorias ou
especificações.
SÉRIES ESPECÍFICAS
SÉRIES CONJUGADAS OU TABELA
DE DUPLA ENTRADA.
Neste tipo de Série poderemos
ter mais de uma variável
sofrendo variações.
SÉRIES CONJUGADAS ou TABELA
DE DUPLA ENTRADA.