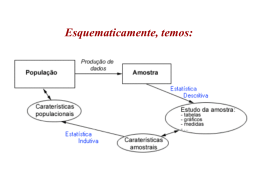
A Influência da Amostragem na
Representatividade dos Dados
por
Manuel Rui F. Azevedo Alves
ESTG - Instituto Politécnico de Viana do Castelo
REQUIMTE – Rede de Química e Tecnologia
Sumário
Tópico 1: Definições importantes
Tópico 2: A amostragem aleatória simples
- A precisão dos resultados
- O tamanho da amostra
- Os problemas da amostragem
Tópico 3: Amostragens alternativas
- Amostragem estratificada
- Amostragem por clusters
- Amostragem multi-etápica
- Amostragem sequencial
Tópico 4: Equacionar o tamanho da amostra e a redução do trabalho
2ª REUNIÃO DA REDE PORTFIR
Definições Importantes
População – Um conjunto de unidades, normalmente infinito, ou
infinito para efeitos práticos, cujas características se pretende estimar.
A média da população indica-se por μ, o desvio padrão por σ e o
tamanho da população por N.
Amostra – Um conjunto de unidades retiradas da população que se
destinam a ser efectivamente estudadas. Estas unidades chamam-se
unidades amostrais. O tamanho da amostra indica-se por n, a média
da amostra indica-se por e o desvio padrão por s.
Unidades analíticas – São porções de alimentos, normalmente
provenientes de unidades amostrais, que são efectivamente
consumidas nas análises. Se bem homogeneizadas, os resultados
obtidos para as unidades analíticas são válidos para as unidades
amostrais.
Definições Importantes (2)
μ,σ,N
Amostragem Aleatória Simples
Uma amostra diz-se aleatória se qualquer das unidades populacionais
tem igual oportunidade de ser seleccionada para a amostra. Dito por
outras palavras, se todas as amostras do mesmo tamanho, possíveis
de retirar da população, têm igual oportunidade de serem
seleccionadas.
Por exemplo, se uma população for constituída por N=1000 unidades
e se retirar uma amostra de n=5 unidades, há C(1000:5) = 8,25×1012
amostras diferentes possíveis. A probabilidade de retirar uma dessas
amostras é 1/ C(1000:5) = 1,2×10-13.
É necessário dispor de métodos que garantam que o processo de
selecção das unidades para a amostra é realmente aleatório: usando a
máquina de calcular (ran#), uma tabela de números aleatórios, etc.
Cálculos Efectuados a Partir dos Parâmetros Amostrais
a média da amostra:
1
= × ∑=1 ∑=1 − 2
desvio padrão da amostra:
=
erro padrão da estimativa da média:
=
estimativa da média da população:
− ≤ ≤ + notação alternativa para a estimativa:
− × /√ ≤ ≤ + ×/√
notas:
−1
0.5
√
n é o tamanho da amostra, i.e., número de unidades amostrais
t é um valor da distribuição t de student que origina um grau de confiança
a precisão depende sempre do trabalho efectuado
Cálculos Efectuados a Partir dos Parâmetros Amostrais: Exemplo
Amostra de 5 teores de proteína
Dados:
20, 22, 25, 25, 21
a média da amostra:
=
20+22+25+25+21
5
= 22,6
20−22,6 2 +⋯+21−22,62
desvio padrão da amostra:
=
erro padrão da estimativa:
=
intervalo de confiança de 95%:
t = 2,78
2,3
√5
4
0.5
= 2,3
= 1,03
estimativa do teor proteico da população:
22,6 − 2,78 × 1,03 ≤ !"# $! %#"!í' ≤ 22,6 − 2,78 × 1,03
19,74 ≤ !"# $! %#"!í' ≤ 25,46
As Questões Que Têm de Ser Respondidas Antes de Iniciar o Trabalho
Um investigador que vai efectuar um trabalho de campo, vai querer saber:
- Qual o tamanho de amostra que tem de ser recolhido?
- Qual o tipo de amostragem a efectuar?
- Qual o método de análise?
Para responder a estas questões, é necessário definir:
- Qual o erro que se considera admissível, absoluto, ou expresso percentagem da média?
- Qual a probabilidade de errar que estamos dispostos a aceitar?
- Qual o conhecimento que existe sobre o tema?
Nota:
Em geral, quem pergunta sobre como proceder sob o ponto de vista estatístico, nunca
coloca todas as questões relevantes e quando obtém os resultados práticos, vai querer
com esses resultados dar respostas a mais algumas perguntas…
Noção de Distribuição Amostral com Média e Desvio Padrão Conhecidos
Temos confiança que o valor de 1 unidade = µ ± z × σ
Temos confiança que o valor médio de n unidades = µ ± z × σ /√
Noção de Distribuição Amostral: Exemplo
Temos 95% de confiança que o teor proteico de 1 unidade = 22,6 ± 6,39
Temos 95% de confiança que o teor proteico médio de 5 unidades = 22,6 ± 2,86
Determinação do Tamanho da Amostra
As Questões Que Têm de Ser Respondidas Antes de Iniciar o Trabalho
Um investigador que vai efectuar um trabalho de campo, vai querer saber:
- Qual o tamanho de amostra que tem de ser recolhido?
- Qual o tipo de amostragem a efectuar?
- Qual o método de análise?
Para responder a estas questões, é necessário definir:
- Qual o erro que se considera admissível, absoluto, ou expresso percentagem da média?
- Qual a probabilidade de errar que estamos dispostos a aceitar?
- Qual o conhecimento que existe sobre o tema?
As Questões Que Têm de Ser Respondidas: Exemplo
Um investigador que vai efectuar um trabalho de campo para determinar a composição
química da fiambrina (filete afiambrado), vai querer saber:
Pergunta:
-Qual o erro que se considera admissível como resultado do estudo que se vai fazer?
Resposta:
-Não mais do que 10% do valor real de cada parâmetro analisado.
Pergunta:
- Qual a probabilidade de errar que está disposto a aceitar? 5 vezes em cada 100?
Resposta:
Estou indeciso entre 1 em cada 100 e 5 em cada 100.
Pergunta:
- Qual o conhecimento que existe sobre o tema? Qual a variação esperada? E a média?
Resposta:
- A média é capaz de rondar os 20 e o desvio padrão ronda 10 (g/100g)
Amostragem Estratificada
•
•
•
•
•
A população é heterogénea, mas as partes que a constituem podem ser
homogéneas. Considera-se então que a população está dividida em
subpopulações, ou estratos. Não há sobreposições entre os estratos.
Em cada estrato procede-se a uma amostragem aleatória simples, o que conduz à
amostragem estratificada aleatória.
Para ter benefício com esta abordagem, é necessário conhecer os tamanhos das
subpopulações e proceder a retiradas de amostras proporcionais aos tamanhos
dos estratos.
Os resultados dentro de cada estrato são muito pouco variáveis, variações
apreciáveis podem existir apenas entre estratos.
Conseguem-se ganhos de precisão e, em geral, a amostragem é mais fácil, sob o
ponto de vista administrativo, desde que os estratos estejam bem definidos.
Amostragem Sistemática
•
•
•
•
•
•
As unidades da população estão acessíveis e podem ser numeradas de 1 a N.
Retira-se ao acaso uma primeira unidade e em seguida, a cada k unidades, é
retirada 1 unidade até perfazer as n unidades da amostra. Conforme os métodos, a
retirada pode ou não ser aleatória dentro de cada conjunto de k unidades.
A amostra tende a ser muito representativa da população e com menor variância
pois na verdade a população é estratificada no processo de amostragem.
Se a população é heterogénea, mas as partes que a constituem podem ser
homogéneas. Considera-se então que a população está dividida em
subpopulações, ou estratos. Não há sobreposições entre os estratos.
Se em cada estrato se procede a uma amostragem aleatória simples, conduz à
amostragem estratificada aleatória, com definição automática de estratos.
O método tem a vantagem de tornar fácil a selecção da amostra e de contribuir
para o aumento da precisão.
Amostragem por Clusters
•
•
•
•
A população é naturalmente constituída por grupos ou clusters.
Supõe-se que os grupos são homogéneos e de dispersão igual à da população, i.e.,
os grupos podem ser visualizados como mini populações.
Procede-se a uma selecção aleatória dos grupos e todas as unidades de cada
grupo seleccionado são estudadas.
Tenta evitar custos relativos ao desconhecimento da população.
Amostragem Multi-etápica ou Multi-fásica
•
•
Este tipo de amostragem consiste em primeiro seleccionar um conjunto de
amostras, as quais não são estudadas completamente. É feita uma amostragem
dentro de cada amostra e só as sub-amostras dentro de cada amostra é que são
analisadas.
Pode aumentar-se o número de divisões, ou etapas, de acordo com as situações.
Muito apropriado a situações em que se podem analisar pequenas quantidades de
material, como é o caso da química, física, etc., com grandes ganhos de precisão
ao poder alargar o âmbito do estudo.
Permite homogeneizar e juntar sub-amostras, minimizando as análises a efectuar.
•
Esquema de amostragem com duas etapas:
•
•
• Obrigado
• Bom encontro