Estatística
1ª Nota de Aula
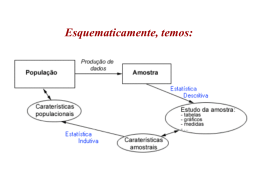
POPULAÇÃO E AMOSTRA
Entende-se por população o conjunto de objetos, itens ou eventos com alguma característica ou
propriedade comum mensurável, ordenável ou comparável de acordo com os limites propósitos e
objetivos do estudo. Sendo assim, formam-se um conjunto de elementos que formam o universo
que é passível de serem observados, sob as mesmas condições.
Podem se classificar em População Finita e População Infinita
População Finita: é aquela que se consegue enumerar todos os elementos que a formam.
Refere-se a um universo limitado em uma dada unidade de tempo. Exemplificando pode-se dizer
que a quantidade de automóveis produzidos por uma fábrica em um mês, a população de uma
cidade e o número de alunos de uma sala de aula são exemplos de uma população finita.
População Infinita: é aquela cujos elementos não podem ser contados. Refere-se a um universo
não delimitado. Os resultados (cara ou coroa) obtidos em sucessivos lances de uma moeda, o
conjunto dos números inteiros, reais ou naturais são exemplos de populações infinitas.
Como em qualquer estudo estatístico tem-se em mente pesquisar uma ou mais características
dos elementos de alguma população, esta característica deve estar perfeitamente definida. E isto
se dá quando, considerado um elemento qualquer, podemos afirmar, sem ambigüidade, se esse
elemento pertence ou não à população.
Na maioria das vezes, por impossibilidade ou inviabilidade econômica ou temporal, limitamos as
observações referentes a uma determinada pesquisa apenas uma parte da população. A essa
parte proveniente da população em estudo denominamos amostra
Amostra é qualquer um de seus possíveis subconjuntos. Ao menor desses subconjuntos dá-se o
nome de unidade amostral. Ou seja, é um subconjunto finito de uma população. Toda amostra é
um conjunto extraído da população.
Pergunta-se por que estudar amostras em lugar de populações. No caso da escolha por uma
amostra que não represente bem o todo, iremos fazer predições inexatas ao tentar estimar as
características da população com base na amostra. Esse risco não correrá se for estudada toda a
população. Há, entretanto, várias razões por que se estudam amostras em lugar do todo. A mais
importante é o custo excessivo e/ou a dificuldade de estudar toda a população.
Estatística
1ª Nota de Aula
Atenção:
1. Como é dispendioso, difícil e por vezes impraticável ter acesso a toda uma população,
costuma-se escolher uma amostra e estudá-la.
2. Para evitar predições imprecisas, é essencial que a amostra represente efetivamente a
população da qual foi extraída.
AMOSTRAGEM
A amostragem – inspeção de parte da população – é mais econômica mais rápida (reduz o
número de dados), incomoda menos ( consulta menor número de pessoas) e pode até apresentar
resultados mais confiáveis: é que poucas consultas permitem contar com pessoal especializado,
mais bem qualificado.
Grande parte das pesquisas cientifica ou de resoluções de problemas de engenharia é feita por
amostragem, ou seja, observamos apenas um subconjunto de elementos da população. A
amostragem é particularmente interessante:
1. a população é grande ou infinita;
2. as observações ou mensurações têm alto custo;
3. as medidas exigem testes destrutivos;
4. há necessidade de rapidez etc.
Em geral, o uso de amostragem leva à redução de custos e tempo. Mas a amostragem precisa
ser feita com critérios, pois pretendemos ter amostras que permitam, a partir de uma análise
estatística apropriada, obter conclusões satisfatórias sobre toda a população.
Existem várias técnicas de amostragem, cada uma tem vantagens e desvantagens, e a escolha
deverá ser feita pelo pesquisador de acordo aos objetivos propostos pela pesquisa. Os principais
modelos de amostragem probabilística são: a amostragem aleatória simples, a amostragem
estratificada proporcional e amostragem sistemática. Os principais modelos de amostragem não
probabilística são: a amostragem acidental, a amostragem de voluntários, a amostragem por
escolhas racionais, a amostragem por julgamento do especialista
1. Amostragem Aleatória Simples
Para a seleção de uma amostra aleatória simples, precisamos ter uma lista completa dos
elementos da população. Este tipo de amostragem é equivalente a um sorteio lotérico.
Estatística
1ª Nota de Aula
A amostragem aleatória simples tem a seguinte descrição: Qualquer subconjunto da população,
com o mesmo número de elementos, tem a mesma probabilidade de fazer parte da amostra.
A seleção de uma amostra aleatória simples pode ser facilitada com o uso de números aleatórios,
ou seja, números resultantes de sucessivos sorteios do conjunto { 0,1 ,2, 3 .... 9}
2. Amostragem Sistemática
Quando os elementos da população já se acham ordenados, não há necessidade de construir o
sistema de referência. São exemplos os prontuários médicos de um hospital, os prédios de uma
rua, as linhas de produção etc. Nestes casos, a seleção dos elementos que constituirão a amostra
pode ser feita por um sistema imposto pelo pesquisador. A esse tipo de amostragem
denominamos sistemática.
Assim, no caso de uma linha de produção, podemos a cada dez itens produzidos, retirar um para
pertencer a uma amostra da produção diária. Neste caso, estaríamos fixando o tamanho da
amostra em 10% da população.
3. Amostragem Estratificada
A técnica da amostragem estratificada consiste em dividir a população em subgrupos, que
denominaremos de estratos. Esses estratos devem ser internamente mais homogêneos do que a
população toda, com respeito Às variáveis em estudo. Por exemplo, se para estudar a dureza de
certos aços temos corpos de prova de dois fornecedores, então a população dos corpos de prova
pode ser dividida em dois estratos.
Sobre os diversos estratos da população são realizadas seleções aleatórias de forma
independente.
Amostragem estratificada proporcional: a proporcionalidade do tamanho de cada estrato da
população é mantida na amostra. Por exemplo, se um estrato abrange 20% da população, ele
também deve abranger 20% da amostra.
Amostragem estratificada uniforme: selecionamos o mesmo número de elementos em cada
estrato. É o processo usual quando se deseja comparar os diversos estratos.