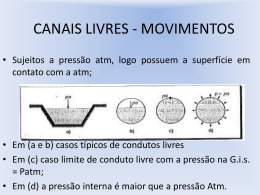
Análise diferencial do
escoamento (Equações de
Navier-Stokes)
Prof. Carlos Ruberto Fragoso Júnior
1:05
Equação da quantidade de movimento
A EQM se torna, nas 3 direções:
  2u  2u  2u 
 u
u
u
u 
p
   u  v  w   g x     2  2  2 
x
y
z 
x
z 
 t
 x y
  2v  2v  2v 
 v
v
v
v 
p
   u  v  w   g y     2  2  2 
x
y
z 
y
 t
 x y z 
 2w 2w 2w 
 w
w
w
w 
p
   u  v  w   gz     2  2  2 
x
y
z 
z
y
z 
 t
 x
2:52
Equação da quantidade de movimento
Casos particulares
- Escoamento permanente:
  2u  2u  2u 
 u
u
u 
p
  u  v  w   g x     2  2  2 
y
z 
x
z 
 x
 x y
  2v  2v  2v 
 v
v
v 
p
  u  v  w   g y     2  2  2 
y
z 
y
 x
 x y z 
 2w 2w 2w 
 w
w
w 
p
  u  v  w   gz     2  2  2 
y
z 
z
y
z 
 x
 x
2:52
Equação da quantidade de movimento
Casos particulares
- Escoamento bidimensional (w=0):
  2u  2u 
 u
u 
p
  u  v   g x     2  2 
y 
x
y 
 x
 x
  2v  2v 
 v
v 
p
  u  v   g y     2  2 
y 
y
 x
 x y 
2:52
Equação da quantidade de movimento
Casos particulares
- Escoamento unidimensional (v=w=0):
2

u

p

u


  u   gx    2
x
x
 x 
2:52
Exercício

2:52
Lista de exercícios.
Coordenadas polares
A Equação da continuidade:
 1  rv z  1  v   v z 



0
t r r
r 
z
2:52
Coordenadas polares
A EQM se torna, nas 3 direções:
 vr
 1   vr  vr 1  2vr 2 v  2vr 
vr v vr v2
vr 
p
    g r   
 
 vr

  vz
 2
 2
r
 2  2
2

t

r
r


r

z

r
r

r

r
r
r


r


z 





v v v v v
v
 v
    vr      r   vz 
r
r 
r
z
 t
 1   v
1 p





g



r


r 

 r r  r
2
2
 v 1  v 2 vr  v 
 2
 2 
 2  2
2
r 
r  z 
 r
 1   vz  1  2vz  2vz 
vz v vz
vz 
p
 vz

 vr

 vz
 2
    g z   
r
 2
2
r r 
z 
z
z 
 t
 r r  r  r 
2:52
Exercício
 r2 
V  Vmax 1  2 
 R 
2:52
Exercício
Na instalação abaixo, a esteira móvel tem uma velocidade periférica U,
transportando . Sendo o peso a única força de campo que atua no
escoamento, determine a vazão q em função da espessura de fluído entre
a esteira móvel e o plano inclinado (e), da diferença de altura entre a
entrada e a saída (h) e do comprimento total da esteira (L).
h
y
x
θ
L
2:52
Exercício
Uma placa larga movendo-se com velocidade vertical, passa através de
um recipiente que contém em líquido viscoso. Devido às forças viscosas a
esteira “pega” uma lâmina de fluído de espessura h. A gravidade tende a
drenar o fluído para baixo. Determine a expressão de velocidade da lâmina
de fluído. Considere o escoamento permanente, laminar e uniforme.
h
g
y
V0
x
2:52