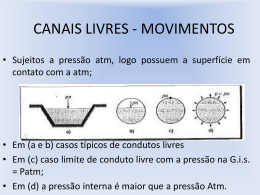
CANAIS LIVRES - MOVIMENTOS
• Sujeitos a pressão atm, logo possuem a superfície em
contato com a atm;
• Em (a e b) casos típicos de condutos livres
• Em (c) caso limite de conduto livre com a pressão na G.i.s.
= Patm;
• Em (d) a pressão interna é maior que a pressão Atm.
TIPOS DE MOVIMENTOS -ESCOAMENTOS
• Escoamento Permanente – Na seção v. e Q constante em
grandeza e direção;
• Escoamento Permanente Uniforme – Seção uniforme, h e v
constante;
• Esc. Perm. Variado – Aceleração ou retardo do escoamento (
gradual ou brusco);
• Escoamento não permanente – Vazão variável.
Considerações:
• Para escoamento permanente o volume de entrada tem de ser
constante;
• Aumento da declividade resulta em aumento da velocidade,
reduzindo-se a profundidade. Isto acarretará um aumento da
resistências de atritos, sempre de maneira a manter o balanço
de forças;
• Em caso de escoamento uniforme, a linha de água = linha do
fundo do canal.
CARGA ESPECÍFICA
• Carga total existente numa seção:
𝐻𝑡 = 𝑍 + 𝑌
𝑣2
+ 2𝑔
• Em seções de jusante a carga total será menor, pois o
Z vai se reduzindo, permitindo a manutenção do
escoamento contra os atritos.
• Escoamento uniforme não existe na natureza, apenas
se aproximam, mesmo em canais prismáticos;
• Nas extremidades a profundidade (h) e a velocidade
(v) são variáveis;
• O escoamento uniforme pode passar a variado, em
consequência de mudanças de declividade, variação
da seção e presença de obstáculos;
• A resistência oferecida pelas paredes e pelo fundo
reduz a velocidade, bem como os ventos e a
resistência atmosférica;
DISTRIBUIÇÃO DE VELOCIDADES
SEÇÃO TRANSVERSAL
• Vmáx na vertical 1;
• Curvas isotáquicas = linhas com pontos de igual v;
SEÇÃO LONGITUDINAL:
• Figura mostra variação de v;
• Considerando vméd na seção = 1, temos o diagrama
de variação de velocidades com a profundidade:
• vméd na vertical equivale de 80 a 90 % da v
superficial;
ÁREA MOLHADA, PERÍMETRO
MOLHADO E RAIO HIDRÁULICO
• Área molhada (A) – área útil de escoamento numa
seção. Medição em m2;
• Perímetro molhado (P) – linha que delimita a área
molhada junto as paredes e ao fundo. Não abrange a
superfície livre. Medido em m;
• Raio Hidráulico (RH) – razão entre a área molhada e o
perímetro molhado. Medido em m.
EQUAÇÃO GERAL DA RESITÊNCIA
Tome-se um trecho de comprimento unitário, mov.
Unitário, velocidade depende da inclinação que será a
mesma da linha de água. Sendo o peso específico da
massa líquida, a força que produz o movimento será a
componente tangencial o peso do líquido.
𝑭 = 𝜰 ∗ 𝑨 𝐬𝐢𝐧 𝜶
(equação 1)
EQUAÇÃO GERAL DA RESISTÊNCIA AO
ESCOAMENTO
• Para movimento uniforme, a força (F) deve se
contrabalancear com a resistência oposta ao
escoamento resultante dos atritos que pode ser
considerada proporcional aos seguintes fatores:
1. Peso específico do líquido (𝜰);
2. Perímetro molhado (P);
3. Comprimento do canal (=1);
4. Função φ(v) da velocidade média.
Res = 𝜰*P* φ(v)
(equação 2)
FÓRMULA DE CHÉZY
• Em 1775, Chézy propôs uma a seguinte expressão:
𝑣 = 𝐶 𝑅 𝐻𝐼
(equação 3)
• Lembrando da equação da continuidade:
𝑄 =𝑣∗𝐴
(equação 4)
• COEFICIENTE DE MANNING
1
1
𝐶 = 𝑅𝐻 6
𝑛
𝑛 = coeficiente de rugosidade de Ganguillet e Kutter quadro 16.2
– Azevedo Netto 8° edição.
• FÓRMULA DE MANNING
2
𝑛∗𝑄
= 𝐴 ∗ 𝑅𝐻 3
𝐽
(equação 5)
ou 𝑣
Q = vazão (m3/s);
I=J=declividade do fundo canal (m/m);
A = área molhada (m2);
RH = raio hidráulico (m).
2
1
= ∗ 𝑅𝐻 3
𝑛
(equação 6)
∗ 𝐼
1
2
• A formula de Chézy, utilizando o coeficiente de Manning
é a mais utilizada, por ter sido experimentada desde os
canais de dimensões pequenas até os grandes, com
resultados coerentes entre o projeto e a obra.
• São três os problemas hidraulicamente determinados
que para qualquer tipo de canal , ficam resolvidos com
Chézy + Manning, sendo:
1. Dados n, A, RH e I, calcular Q;
2. Dados n, A, RH e Q, calcular I;
3. Dados Q e I calcular A e RH.
Já o caso do problema 3 usando a equação 5, a solução é
bastante laboriosa, pois é um dimensionamento
geométrico do canal. Segue resolução.