Produto Vetorial
Produto Vetorial
Para definir o produto vetorial entre dois vetores
é indispensável distinguir o que são bases
positivas e bases negativas
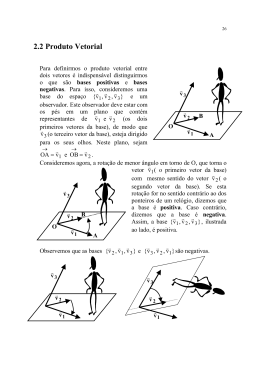
Para isso, considere uma base do espaço
{v1, v2 , v3} e um observador
O observador deve estar com os pés em um
plano que contém representantes de v1 e v2 (os
dois primeiros vetores da base)
v3 (o terceiro vetor da base), esteja dirigido para
os seus olhos
Produto Vetorial
No exemplo considere OA =v1 e OB =v2
Considere agora, a rotação de menor ângulo em torno
de O, que torna o vetor v1 ( o primeiro vetor da base)
com mesmo sentido do vetor v2 ( o segundo vetor)
Se esta rotação for no sentido contrário ao dos ponteiros
de um relógio (anti-horário), dizemos que a base é
positiva
Caso contrário (sentido horário), a base é negativa.
Assim, a base {v1, v2 , v3}, do exemplo, é positiva
A base {v2 , v1, v3} é positiva?
E {v3 , v2 , v1}?
Produto Vetorial
Note que nem sempre o observador está no
mesmo semi-espaço que nós
Neste caso, o sentido da rotação que ele verá é
contrário ao que nós vemos
Para ilustrar este fato, desenhe em uma folha de
papel dois vetores LI com a mesma origem e
considere uma rotação que torna um deles com
mesmo sentido do outro
Produto Vetorial
A folha de papel pode ser considerada com um
plano, assim, a folha
de papel divide o espaço em dois semi-espaços
Note que, em um desses semi-espaços vemos
esta rotação com um sentido. Se mudarmos de
semi-espaço vemos esta rotação com um
sentido contrário ao anterior
Esta observação é útil na identificação de bases
positivas e negativas, quando o observador não
está no mesmo semi-espaço que nós
Por exemplo, ao analisar a base {v2 , v1,- v3}
vemos a rotação no sentido horário, porém o
observador, por estar no semi-espaço distinto
do qual nos encontramos, vê esta rotação no
sentido anti-horário
Portanto esta base é positiva.
Exemplo
Considere o sistema {O, i, j, k}
Exemplo
Quais as bases positivas e negativas?
Exemplo
As bases {i , j, k}, { j, k, i} e {k, i , j} são
positivas.
As bases { j, i , k}, {i , k, j} e {k, j, i} são
negativas.
Produto Vetorial
Definição: Sejam u e v vetores não
colineares.
O produto vetorial de u por v, indicado
u x v, é um vetor, tal que:
|
u x v |= | u | | v | sen(u, v)
O vetor u x v é ortogonal ao plano que
contém representantes dos vetores u e v
A base {u, v, u x v} é positiva
Exemplo
Sejam u e v vetores com representantes
no plano alpha , onde | u |= 2, | v |= 3
e (u, v) = 30º
| u x v | = | u || v | sen 30º=
=2
3
½= 3
| v x u | = | v | | u |sen 30º=
½
32= 3
Exemplo
|u x v| = |v x u|, mas estes vetores são
opostos
Exemplo 3
Dada a base ortonormal positiva {i, j, k}
i x i= j x j= k x k= 0
i x j= k, j x k =i e k x i= j
j x i =-k, k x j=- i e i x k=- j
Interpretação Geométrica
Consideremos o paralelogramo ABCD,
Interpretação Geométrica
Sabemos que a área S desse
paralelogramo é:
S = base x altura, ou seja S = | AB | × h.
Do triângulo AMD, temos:
h =| AD | sen teta
Interpretação Geométrica
S = | AB | |AD | sen teta
S =| AB x AD|
Interpretação Geométrica
Encontre a área do triângulo ABD
S = |AB | |AD | sen teta
S =|AB x AD|
Logo a área do triângulo é |AB x AD|/2
Exemplo 4
Encontre a área do paralelogramo, onde
A(1,1,0), B(0,1,2) e C(4,1,0)
| AB| =| (-1,0,2)| = 5
| AD| =| (4,0,-2)|= 2 5
Cos(AB,AD) = (AB.AD)/(|AB||AD|) = -4/5
Sen2x + cos2 x =1
Sen(AB,AD)=3/5
S = 5 3/5 2 5 = 6 u.a.
Propriedades
Considere u, v e w vetores quaisquer e t
um número real
1) u x v = v x u
2) (t v) x u = v x(t u) = t (v x u)
3) u x (v + w)= u x v + u x w
Expressão cartesiana do produto
vetorial
Dados uma base ortonormal positiva
{i, j, k} e dados os vetores u = (x1, y1, z1) e
v = (x2 , y2 , z2 )
u x v = (x1i + y1j + z1k) x (x2i + y2j + z2k)
=(x1x2 ) ixi + (x1y2 ) ixj + (x1z2 ) ixk+
+(y1x2 ) jxi + (y1y2 ) jxj + (y1z2 )jxk+
+(z1x2) kxi + (z1y2 ) kxj+ (z1z2) kxk
Expressão cartesiana do produto
vetorial
u x v = (y1z2-y2z1)i + (z1x2-z2x1)j +
(x1y2-x2y1)k
Exemplo 5
Dados os vetores u = (1,2,3), v = (3,1,2) e
w = (2,4,6), calcule:
uxv=?
uxw=?
Exemplo 5
Dados os vetores u = (1,2,3), v = (3,1,2) e
w = (2,4,6), calcule:
u x v = (4-3) i + (9-2) j + (1-6) k = (1,7,-5)
u x w = (12-12)i+(6-6)j+(4-4)k = (0,0,0)=0
Exemplo 6
Observe os paralelogramos ABCD e ABC’C
Exemplo 6
S e S’ são as áreas dos paralelogramos
ABCD e ABC’C, respectivamente
Determine a relação de S e S’
Exemplo 6
S e S’ são as áreas dos paralelogramos
ABCD e ABC’C, respectivamente
S =| AB x AD|
S’ =| AB x AC|
| AB x AC|= | AB x (AB+ BC) |=
Exemplo 6
| AB x(AB +BC)|= | AB x AB + AB x BC|
=| 0 + AB x AD|
= | AB x AD| = S
Exemplo 7
Determine a área S do retângulo, onde
A(1,0,2), C(- 2,3,3) e AB° = (-1,0,0)
S =| AB x AC| e AC = (- 3,3,1)
Como AB _ BC, temos que AB= projABº AC
=(-3,0,0)
S =| (- 3,3,1)x(- 3,0,0)| =| ( 0,-3, 9 )| =
9 81 3 10
Baixar