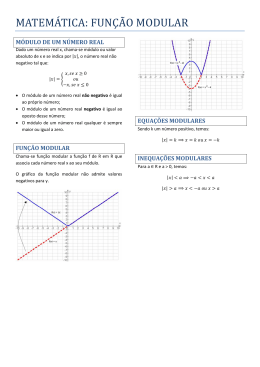
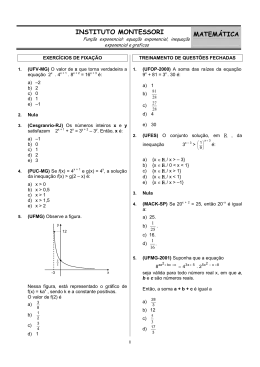
COLÉGIO MACHADO DE ASSIS
Disciplina: Matemática
Professor: Alexandre Machado Vieira
Turma: 1º ano ___
Data:
Aluno(a):
/
/
Nº:
ROTEIRO DE ESTUDO PARA A RECUPERAÇÃO DO 3° TRIMESTRE
Conteúdos: Função quadrática; Equação e inequação do 2° grau; Função e equação modular.
Estudar os exercícios da apostila trabalhados em sala.
EXERCÍCIOS COMPLEMENTARES
1. A expressão que define a função quadrática f(x), cujo gráfico está esboçado,
é:
2.
Sendo f : R  R uma função definida por f(x) = x2 –1, calcule:
a)
3.
 1
f 
2
b)

f 1 2

A função real f, de variável real, dada por f(x) = x2 + 2x + 4, responda:
a. Qual a coordenada onde o gráfico encontra o eixo y?
b. Quais são as raízes da função?
c. Qual o ponto máximo ou mínimo da função?
d. Faça o esboço do gráfico dessa função.
4.
Determine o conjunto solução da seguinte inequação:
2x  5x  4  7  x  2x  3
5. Dada a função modular y = 2 + |x – 1|, responda:
a. Calcule f(1) e f(  ).
b. Escreva a lei que define a função sem módulo, assumindo para todo x real.
6. Resolva as seguintes equações modulares.
a. |x + 2 | = |x + 1|
b. |4 + x| = x – 4
7. Sejam p e q raízes da equação |3x + 15| = 12. Encontre o valor de |2p – q|.
8. Esboce o gráfico das seguintes funções modulares:
a.
f(x) = |x2 + x – 2|
b. f(x) = |x + 2| + 1
c. |x 2 - 1| = 8