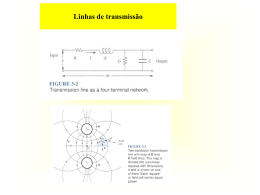
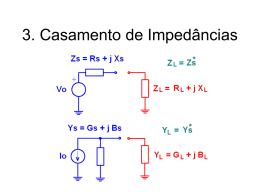
Linhas de transmissão
• Tensão e corrente ao longo da linha
V y   Vi 2  e y  k s e  y 


I y  
Vi 2  y
 y 
 e  ks e


Z0 
k s  k e j- factor de reflexão na carga
• Impedância de entrada da linha
1  k s e  2l
Zin 
 Z0
I ( y l )
1  k s e  2l
V ( y l )
• Impedância à distância y da carga
1  k s e  2y
Z y  Z0
1  k s e  2y
• Impedância normalizada
1 k y
zy 
1 k y
• Coeficiente da reflexão à distância y da carga
V ry k s e  y

2

y
k y  ks e


 k e j e  2 y  k e jy
Viy
e y
 y    2 y
• Impedância normalizada zy:
1 k y
zy 
1 k y
A equação:
a)
zy 
1 k y
1 k y
Estabelece a relação entre a impedância normalizada e o factor de reflexão, em
qualquer ponto da linha.
k y  k s e  2y  k e j   2y 
• zy e ky são números complexos
z y  r  jx
k y  u  jv
- zy e ky podem ser representadas nos respectivos planos complexos r, x e u,v.
- A equação
zy 
1 k y
1 k y
estabelece a equivalência entre pontos nos dois planos
complexos.
- A representação do plano zy no plano ky está ilustrada na figura.
Carta de Smith – linha sem perdas
 z y  r  jx



 j 2l
k y  k s e


k y  u  jv

zy 
1 k y
1 k y
p
ou
2

r 
1
2
 u 
 v 
 1  r 
1  r 2



1 2 1


2
u  1   v  x   2
x

1 k
1 k
r  jx 
ky 
1  u  jv 
1  u  jv 
z y 1
z y 1
I) A partir da impedância obter o coeficiente de reflexão ks e viceversa
r 0 
u 2  v2  1
a) Impedância
r  
u  12  v 2  0
k y  ks  k
b) Da impedância na carga zs obter ks
O eixo mede-se na escala exterior

  medianosna carta
4

 2 rad
2
II) Transformar impedâncias ao longo da linha
À medida que y varia a fase de ky varia. Mudar a posição ao longo da linha significa, por
isso, na carta de Smith um movimento ao longo dos círculos que têm a origem no plano ky.
O ângulo varia de forma proporcional a β l (comprimento eléctrico). Escala exterior da
carta.
O movimento em relação ao gerador (y aumenta) (e-2βy) conduz a um movimento no sentido
dos ponteiros do relógio.
Transformação de impedâncias – exemplo
zs  1  j1
l

(90º )
4
180º na carta
zin  0.5  j0.5
III) Determinar o factor de onda estacionária p e a posição de um máximo de tensão (e o
inverso) a partir da impedância
zmáx

Vmáx em Vmáx
a impedância é real
z   r 
x  0
k y  k  é real
ky  ky  k
z y 
1 k
p
1 k
Determine zs e a posição l1 de um máximo de tensão
A  1  j1 C l1  0.088  rmáx  p  2.6
Carta de Smith como diagrama de admitâncias
1 1 k y
y 
z 1 k y
As admitâncias transformam-se da mesma maneira que as impedâncias ao longo da linha, é
por isso os procedimentos descritos para impedâncias são válidos para admitâncias.
Os valores lidos na carta são iguais.
Mas é preciso notar as seguintes diferenças:
- o eixo u na parte direita representa agora uma admitância máxima e portanto
uma corrente máxima em vez de uma tensão máxima.
- a fase do factor de reflexão refere-se à relação entre a corrente da onda
reflectida e a corrente da onda incidente e difere assim de π do coeficiente de
reflexão de tensão.