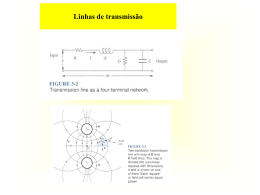
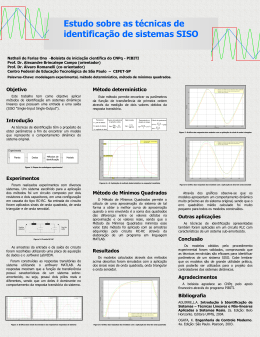
Conceitos Fundamentais – Aula 3

Propagação de Ondas em Dieléctricos

 1

__
__
__
~
~
~
  H  J  j D   E  j E  j  eq E
 eq    j
~
~
~


 Ângulo de perdas do

 
 j      j
2 
dieléctrico:
t g 

 ( 1)

 O efeito das perdas (pequenas) traduz-se no aparecimento de  mas β fica
praticamente inalterado em relação ao caso  = 0.
Impedância característica num bom
dieléctrico
Z ~
 
 
1  j

 
2 
 Num dieléctrico com fracas perdas, a pequena componente de perdas vai fazer
aparecer uma pequena componente reactiva na impedância característica.
Propagação num Bom Condutor

1

 
 
 

j 1  j
~



^
1 j
 

2

e
 n~ . r~
j

1
e 
^
n~ . r~

j
e 
^
n~ . r~
^
n~ direcção de propagação (normal ao plano de fase constante)
•
A onda é muito atenuada á medida que se propaga no meio condutor e a sua desfasagem por
unidade de comprimento também é muito elevada.
•
A velocidade de fase é muito pequena
Impedância característica
num bom condutor
Z
•
j
~
  j
j

1 

R

 m
 

 Rm 1  j 
Num bom condutor em radio frequência a taxa de atenuação é muito elevada e a
onda só penetra uma distância curtíssima, sendo rapidamente reduzida a um valor
insignificante.
•
δ – profundidade na qual a onda já foi atenuada de 1/e
Cobre
(~ 37% do valor inicial)
1MHz
0.0667 mm
100 MHz
0.00667 m
Água do Mar
1MHz
25 m
Água
1MHz
7.1 m

Propagação de Ondas em Dieléctricos

 1

__
__
__
~
~
~
  H  J  j D   E  j E  j  eq E
 eq    j
~
~
~


 Ângulo de perdas do

 
 j      j
2 
dieléctrico:
t g 

 ( 1)

 O efeito das perdas (pequenas) traduz-se no aparecimento de  mas β fica
praticamente inalterado em relação ao caso  = 0.
Impedância característica
num dieléctrico
Z ~
 
 
1  j

 
2 
 Num dieléctrico com fracas perdas, a pequena componente de perdas vai fazer
aparecer uma pequena componente reactiva na impedância característica.
 Propagação num Bom Condutor

1

 
 
 

j 1  j
~



^
1 j
 

2

e
 n~ . r~
j

1
e 
^
n~ . r~

j
e 
^
n~ . r~
^
n~ direcção de propagação (normal ao plano de fase constante)
•
A onda é muito atenuada á medida que se propaga no meio condutor e a sua desfasagem por
unidade de comprimento também é muito elevada.
•
A velocidade de fase é muito pequena
Impedância característica
num bom condutor
Z
•
j
~
  j
j

1 

R

 m
 

 Rm 1  j 
Num bom condutor em radio frequência a taxa de atenuação é muito elevada e a
onda só penetra uma distância curtíssima, sendo rapidamente reduzida a um valor
insignificante.
•
δ – profundidade na qual a onda já foi atenuada de 1/e (~ 37% do seu valor inicial)
Cobre
1MHz
0.0667 mm

100 MHz
0.00667 mm
Água do Mar
1MHz
25 m
Água
1MHz
7.1 m
Dispersão num Meio com Perdas
___
___
2
 E  j   j  E  0
~
~
 jk
~

j   j 


D   , k   k . k  j   j   0
 ~ ~ ~
O vector de onda k
jk  
^
jk n
~
~
num meio com perdas é complexo
~
^
A normal
n~ à frente de onda (plano de fase constante)
 j k  H    j E
~
~
Condutores e Dieléctricos
~
corrente de condução


corrente de deslocamento
Éa razão entre a densidade de corrente de condução e a densidade de corrente de
deslocamento.
Bons condutores (como os
metais)

 1

Cobre
f  30GHz
Bons dieléctricos (ou isoladores)

 1

Mica (em frequências de audio
e radiofrequência)

~ 0.0002


 3.5 10 8

O campo eléctrico de uma onda é dado por:


1
7
E  100cos 10  t x Vm 1 em z  0
~
~
Estude as características de propagação da onda na água do mar :
Mar _  r  72 o
  45 m1
a) Calcule a cte de atenuação
Cte de fase
Impedância da onda no mar
Velocidade de fase
Profundidade de penetração
b) Determine a distância ao fim da qual a amplitude do campo é 1% do valor que
tinha em z=0.
c) Escreva as expressões de E e H em z = 0.8m
~
~
a) Propagação no ar
Comprimento de onda:
 0 , 0 
c
0   60 m
f
Velocidade de fase: c = 3 x 108 m s
Impedância característica

0
120  
0
b) Propagação na água do mar
Mar:
r 

 72; 0 ;  4 S m 1
0
L
Constante de atenuação
Constante de fase


2

Profundidade de penetração
Velocidade de fase
2
Z  (1 j )
2

 8.89 Np m1
 8.89rad m 1
Impedancia característica
Comprimento de onda


  e j / 4 
2
 0.707 m

2


 f   3.53 x 106 ms 1

 0.112 m
Campo à distância de 0.5 m
0 e  z1  0.01
→
Na água do mar a amplitude do campo reduz-se a 1% do seu
valor inicial ao fim de 0.5 m
→
A desfasagem entre o campo eléctrico e magnético é de 45º no
mar e 0º no ar
Propagação no ar e no mar
As características de propagação de uma onda
electromagnética a propagar-se no ar e na água do mar são
substancialmente diferentes.
A onda atenua-se rapidamente na água do mar e não sofre
atenuação no ar.
O campo eléctrico e magnético estão em fase no ar e
desfasados de /4 no mar.
Mesmo em baixas frequências, a comunicação de longa
distância com submarinos é muito difícil.