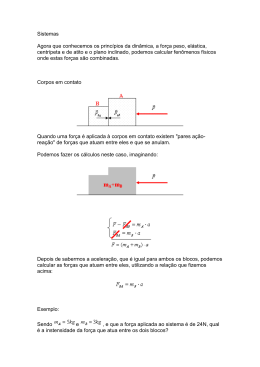
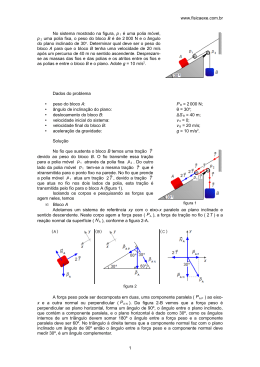
www.fisicaexe.com.br
No sistema da figura ao lado, o corpo A desliza
sobre um plano horizontal sem atrito, arrastado por B
que desce segundo a vertical. A e B estão presos entre
si por um fio inextensível, paralelo ao plano, e que passa
pela polia. Desprezam-se as massas do fio e da polia e
os atritos na polia e no plano. As massas de A e B
valem respectivamente 32 kg e 8 kg. Determinar a
aceleração do conjunto e a intensidade da força de
tração no fio. Adotar g = 10 m/s2.
Dados do problema
•
•
•
massa do corpo A:
massa do corpo B:
aceleração da gravidade:
m A = 32 kg;
m B = 8 kg;
g = 10 m/s2.
Esquema do problema
Escolhemos a aceleração no sentido em que o
corpo B está descendo. Isolando os corpos e
pesquisando as forças que agem em cada um deles
aplicamos a 2.ª Lei de Newton
 = m
F
a
figura 1
Corpo A:
direção vertical:
•
•
PA peso do corpo A;
NA reação normal da superfície.
direção horizontal:
•
figura 2
T tensão na corda.
Na direção vertical o peso e a normal se anulam, não há movimento vertical.
Na direção horizontal aplicando-se a 2.ª Lei de Newton temos a seguinte equação
T = mA a
(I)
Corpo B
•
•
PB peso do corpo B;
T tensão na corda.
Na direção horizontal não há forças atuando, na direção vertical temos
que a 2.ª Lei de Newton nos fornece a equação
P B −T = m B a
(II)
figura 3
Solução
Com as equações (I) e (II) acima temos um sistema de duas equações a dua incógnitas
(T e a), somando as duas equações temos
1
www.fisicaexe.com.br
∣
T = mA a
P B −T = m A a
P B =  m A m B  a
PB
a=
m Am B
(III)
O módulo da força peso do corpo B é dada por
P B = mB g
(IV)
substituindo (IV) em (III) e os valores dados no problema
mB g
m Am B
8 .10
a=
328
80
a=
40
a=
a = 2 m/ s
2
Substituindo a massa do corpo A e a aceleração, encontrada acima, na primeira
expressão a tração no fio vale
T = 32.2
T = 64 N
2