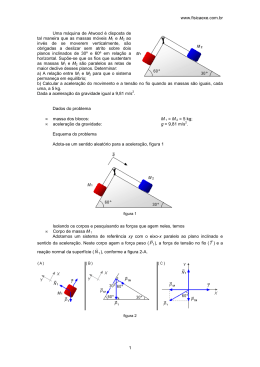
www.fisicaexe.com.br
No sistema da figura ao lado as massas de
A, B e C valem respectivamente 10 kg, 20 kg e 5 kg e
o sen θ = 0,8. Desprezando os atritos calcular a
aceleração do conjunto e a intensidade das forças de
tração nos fios. Adotar g = 10 m/s2.
Dados do problema
•
•
•
•
massa do corpo A:
massa do corpo B:
massa do corpo C:
aceleração da gravidade:
m A = 10 kg;
m B = 20 kg;
m C = 5 kg;
g = 10 m/s2.
Esquema do problema
Escolhemos a aceleração no sentido em
que o corpo A está descendo.
figura 1
Solução
Isolando os corpos e pesquisando as forças que agem em cada um deles aplicamos a
2.ª Lei de Newton
Corpo A:
•
•
•
PA peso do corpo A;
NA reação normal do plano no corpo A;
TAB tensão no fio entre os blocos A e B.
figura 2
Adotamos um sistema de referência xy com o eixo-x paralelo ao plano inclinado e
sentido da aceleração (figura 2-A).
1
www.fisicaexe.com.br
 AP ) ao eixoA força peso pode ser decomposta em duas, uma componente paralela ( P
 AN ). Da figura 2-B vemos que a força peso é
x e a outra normal ou perpendicular ( P
perpendicular ao plano horizontal, forma um ângulo de 90º, o ângulo entre o plano inclinado,
que contém a componente paralela, e o plano horizontal é dado como θ, como os ângulos
internos de um triângulo devem somar 180º o ângulo entre a força peso e a componente
paralela deve ser 90º – θ. No triângulo à direita temos que a componente normal faz com o
plano inclinado um ângulo de 90º então o ângulo entre a força peso e a componente normal
deve medir θ, é um ângulo complementar.
Colocando as forças num sistema de eixos coordenados, figura 2-C, podemos usar a
2.ª Lei de Newton
 = m
F
a
Na direção y não há movimento, a reação normal e a componente normal do peso se
anulam, na direção x, considerando o ângulo θ medido a partir do eixo-y ao contrário do que se
faz usualmente quando se mede o ângulo com o eixo-x, escrevemos
P AP−T AB = m A a
P A sen θ−T AB = m A a
(I)
Corpo B
•
•
•
•
PB peso do corpo B;
NB reação normal da superfície.
TAB tensão no fio entre os blocos A e B;
TBC tensão no fio entre os blocos B e C.
Na direção y o peso e a normal se anulam, não há movimento
vertical. Na direção x aplicando a 2.ª Lei de Newton temos
figura 3
T AB−T BC = m B a
(II)
Corpo C:
•
•
PC peso do corpo C;
TBC tensão no fio entre os blocos B e C.
Na direção horizontal não há forças atuando, na direção vertical temos
que a 2.ª Lei de Newton nos fornece a equação
T BC−P C = m C a
(III)
figura 4
Com as equações (I), (II) e (III) acima temos um sistema de três equações a três
incógnitas (TAB, TBC e a), somando as três equações temos
∣
P A sen θ−T AB = m A a
T AB −T BC = mB a
T BC−P C = m C a
P A sen θ−P C =  m A m Bm C  a
P A sen θ−P C
a=
m A mB mC
(IV)
O módulo das forças peso dos corpos A e C são dadas por
PA = mA g
e
2
PC = mC g
(V)
www.fisicaexe.com.br
substituindo (V) em (IV) e os valores dados no problema
m A g sen θ−mC g
m A m Bm C
10 .10 .0,8−5 .10
a=
10 205
80−50
a=
35
30
a=
35
a=
a = 0,86 m/s
2
Substituindo a massa do corpo A, a expressão para o peso de A dada em (V) e a
aceleração, encontrada acima, na primeira expressão do sistema, a tensão no fio vale
m A g sen θ−T AB = m A a
10. 10.0,8−T AB = 10. 0,86
80−T AB = 8,6
T AB = 80−8,6
T AB = 71,4 N
Substituindo a massa do corpo C, a expressão para o peso de C dada em (V) e a
aceleração, encontrada acima, na terceira expressão do sistema, a tensão no fio vale
T BC −mC g = m C a
T BC−5 .10 = 3 .0,86
T BC−50 = 2,58
T BC = 502,58
T AB = 52,6 N
3