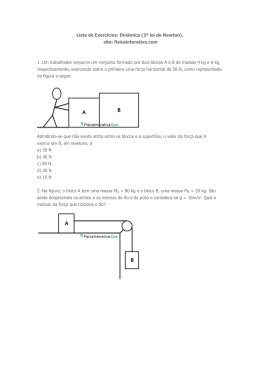
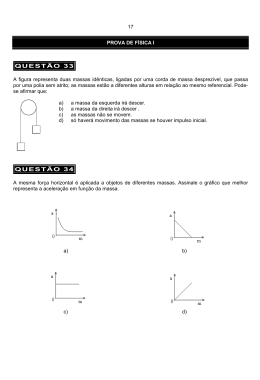
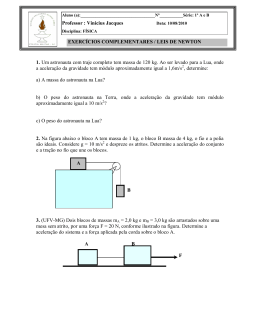
www.fisicaexe.com.br
Dois blocos de massas m A = 0,35 kg e m
=
1,15
kg estão sobre uma superfície horizontal
B
perfeitamente lisa, os blocos estão ligados por um
fio ideal. Uma força horizontal de intensidade
constante igual a 15 N é aplicada puxando os dois
blocos. Calcule a aceleração adquirida pelo conjunto e a tensão no fio que liga os blocos.
Dados do problema
•
•
•
m A = 0,35 kg;
m B = 1,15 kg;
F = 15 N.
massa do corpo A:
massa do corpo B:
força aplicada ao conjunto:
Solução
Isolando os corpos e pesquisando as forças que atuam em cada um deles, temos para
o corpo A
direção horizontal:
•
T: força de tensão no fio.
direção vertical:
•
•
N A: força de reação normal da superfície no corpo;
P A: força peso.
figura 1
Na direção vertical não há movimento, a força normal e a força peso se anulam.
Na direção horizontal aplicando a 2.ª Lei de Newton obtemos
FR = m a
T = mA a
(I)
Para o corpo B, temos
direção horizontal:
•
•
F: força aplicada ao sistema;
-T: força de tensão no fio.
direção vertical:
•
•
N B: força de reação normal da superfície no corpo;
P B: força peso.
figura 2
Na direção vertical não há movimento, a força normal e a força peso se anulam.
Na direção horizontal aplicando a 2.ª Lei de Newton obtemos
F − T = mB a
(II)
As expressões (I) e (II) formam um sistema de duas equações a duas incógnitas (T e a)
T = mA a
F − T = mB a
substituindo (I) em (II) obtemos a aceleração
1
www.fisicaexe.com.br
F − m A a = mB a
F = m A a + mB a
colocando a aceleração a em evidência do lado direito da igualdade
(
)
F = mB + m A a
a=
a=
F
mB + m A
15
0,35 + 1,15
15
a=
1,5
a = 10 m/s 2
observação: o fio que liga os dois blocos é ideal, isto quer dizer que podemos considerá-lo
inextensível e de massa desprezível, a única função do fio é transmitir a força de um bloco para
o outro bloco. Os dois blocos formam um conjunto submetido a mesma força, ambos têm a
mesma aceleração, o sistema se comporta como se fosse um único bloco de massa total dada
pela soma das massas dos dois blocos A e B.
Substituindo a aceleração encontrada na expressão (I) temos a tensão no fio
T = 0,35 .10
T = 3,5 N
observação: analogamente poderíamos substituir a aceleração na expressão (II) para obter a
força de contato, neste caso teríamos:
15 − T = 1,15 .10 ⇒ 15 − T = 11,5 ⇒ T = 15 − 11,5 ⇒ f = 3,5 N
2