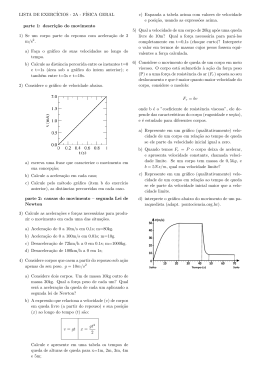
Ufes - Universidade Federal do Espı́rito Santo
Fı́sica I
Lista de exercı́cios : movimento em uma dimensão
1 - Calcule a velocidade média para o percurso completo nas duas seguintes situações:
(a) Um motorista desloca-se 40 km a 80 km/h e mais 40 km a 120 km/h.
(b) Um motorista desloca-se durante 1, 0 h a 60 km/h e depois mais 1, 0 h a 120 km/h.
2 - Um piloto de caça, praticando manobras para não ser detectado por radar, está
voando manualmente na horizontal a 1300 km/h, a apenas 35 m acima do nı́vel do
solo. De repente, o avião se depara com um terreno que tem uma inclinação suave
para cima de 4, 3o, um valor difı́cil de detectar visualmente. Quanto tempo o piloto
tem para fazer uma correção para evitar que o avião se espatife no chão ?
3 - Considere o gráfico velocidade × tempo mostrado na figura abaixo.
(a) Que distância é percorrida de t = 0 s até t = 16 s?
(b) Construa o gráfico aceleração × tempo de t = 0 s até t = 16 s.
v (m/s)
8
4
0
4
12
8
16
t (s)
4 - Considere o tempo médio de reação de um motorista (tempo que decorre entre
perceber um perigo súbito e aplicar os freios) como sendo 7, 00×10−1 s. Um carro com
bons freios, em uma estrada seca, pode ser freado a 6, 00 m/s2 . Calcule a distância
mı́nima que um carro percorre depois que o motorista avista um perigo, quando ele
trafega a:
(a) 30 km/h.
1
(b) 60 km/h.
(c) 90 km/h.
5 - O sinal amarelo em um cruzamento fica ligado durante 3, 00 s. A largura do
cruzamento é de 15, 0 m. A aceleração máxima de um certo carro que se encontra a
30, 0 m do cruzamento quando o sinal muda para amarelo é de 3, 00 m/s2 e ele pode
ser freado a 5, 00 m/s2. Levando em consideração, como na questão anterior, o tempo
de reação do motorista como sendo 7, 00 × 10−1 s, determine:
(a) a velocidade mı́nima que o carro precisa ter na mudança do sinal para amarelo a
fim de que possa atravessar o cruzamento ainda no amarelo.
(b) a velocidade máxima que ainda lhe permite parar antes de atingir o cruzamento.
6 - Uma partı́cula se move ao longo do eixo x segundo a equação x = 50t + 10t2 , onde
x está em metros e t está em segundos.
(a) Determine a velocidade média da partı́cula durante os primeiros 3, 0 s do seu
movimento.
(b) Determine a velocidade instantânea da partı́cula em t = 3, 0 s.
(c) Determine a aceleração instantânea da partı́cula em t = 3, 0 s.
(d) Trace o gráfico da posição × tempo e indique como a resposta para (a) pode ser
obtida a partir desse gráfico.
(e) Trace o gráfico da velocidade instantânea × tempo e indique como a resposta
para (c) pode ser obtida a partir desse gráfico.
7 - Um carro pára em um semáforo. A seguir ele percorre um trecho retilı́neo de
modo que sua distância ao sinal é dada por x(t) = bt2 − ct3 , onde b = 2, 40 m/s2 e
c = 0, 120 m/s3 .
(a) Calcule a velocidade média do carro para o intervalo de tempo t = 0 até t = 10, 0 s.
(b) Calcule a velocidade instantânea do carro para t = 5, 00 s.
(c) Quanto tempo após partir do repouso o carro retorna novamente ao repouso?
8 - Uma chave cai de uma ponte de uma altura de 45 m acima do nı́vel da água. Ela
cai bem em cima de um barco movendo-se com velocidade constante, que estava a
12 m do ponto de impacto quando a chave foi largada. Qual a velocidade do barco?
9 - Uma pedra é largada de uma ponte 50, 0 m de altura acima do nı́vel da água.
Uma outra pedra é lançada verticalmente para baixo 1, 50 s após a primeira ter sido
largada. Ambas atingem a água ao mesmo tempo.
(a) Qual era a velocidade inicial da segunda pedra?
(b) Faça um gráfico da velocidade em função do tempo para cada pedra do instante
em que iniciaram seu movimento até o instante em que atingem a água.
2
10 - Um pára-quedista salta de pára-quedas e cai 50 m livremente. Então o páraquedas se abre, e daı́ em diante ele desacelera a 2, 0 m/s2 até atingir o chão, com
velocidade de 3, 0 m/s.
(a) Quanto tempo o pára-quedista fica no ar?
(b) A que altura ele estava no inı́cio da queda?
11 - Em um certo andar de um edifı́cio, uma pessoa observa um vaso de flores passar
por uma janela primeiro para cima e depois para baixo. O vaso pode ser visto por
um tempo total de 0, 50 s e a altura de alto a baixo da janela é de 2, 0 m. Até que
altura acima do alto da janela o vaso de flores chega?
12 - Dois trens trafegam em sentidos opostos, no mesmo trilho, cada um com velocidade de 30 km/h. Quando eles ficam a 60 km de distância um do outro um pássaro
que voa a 60 km/h voa de um trem até o outro, depois retorna e assim por diante.
(a) Quantas vezes o pássaro alcança cada trem antes da colisão?
(b) Qual a distância percorrida por ele?
Respostas
1 - (a) 96 km/h; (b) 90 km/h.
2 - 1, 3 s.
3 - (a) 1, 0 × 102 m.
4 - (a) 11, 6 m; (b) 34, 8 m; (c) 69, 6 m.
5 - (a) 44, 5 km/h; (b) 51, 0 km/h.
6 - (a) 80 m/s; (b) 1, 1 × 102 m/s; (c) 20 m/s2 .
7 - (a) 12, 0 m/s; (b) 15, 0 m/s; (c) 13, 3 s.
8 - 4, 0 m/s.
9 - (a) 21, 2 m/s.
10 - (a) 17 s; (b) 2, 9 × 102 m.
11 - (a) 2, 3 m.
12 - (a) O número de vezes tende a ∞; (b) 60 km.
3