Gráficos
Lendo e representando a Fı́sica por gráficos
1. Um ciclista parte de um ponto A rumo a um ponto B viajando numa
linha reta com velocidade escalar constante de 10 m/s. No mesmo instante,
parte de B para A outro ciclista que segue a mesma estrada com velocidade constante de 5 m/s. Sendo de 3600 m a distância de A a B quais as
funções horárias dos ciclistas, identificados pelos pontos de partida A e B,
estabelecendo-se a origem das trajetórias em A e orientando-se de A para B?
Em que instante a distância entre os ciclistas é de 40 m?
NOTA IMPORTANTE: uma das maiores fontes de erro em problemas
desse tipo reside na ESCOLHA do referencial. Este problema o escolhe para
você, mas vamos depois escolher um outro e ver que dá na mesma SE FIZERMOS TUDO CONSISTENTEMENTE.
Funções horárias de acordo com o referencial AB:
xA (t) = 10 t
1
(1)
(sai da origem)
xB (t) = 3600 − 5t
(2)
(3600 é a distância inicial e a velocidade é negativa
porque vai na direção contrária)
xA − xB = 40 = 3600 − 5t − 10t ⇒ 15t = 3560 ⇒ t ≈ 237 s
(3)
Agora vamos mudar a DIREÇÃO do eixo:
Como ficam as equações horárias?
xA (t) = −3600 − 10t ,
(4)
xB (t) = 5t
(5)
|xA − xB | = 40 = 5t + 3600 + 10t ⇒ 3560 = 15t ⇒ t ≈ 237 s
(6)
2
NOTE que usamos o módulo pois queremos uma distância nas posições.
2. Vamos agora aprender as mesmas coisas com a queda livre. Lembre-se
ESCOLHA um sistema de referência SEJA CONSISTENTE com ele.
Seja uma pedra de massa m que é deixada cair de uma altura de 100 m.
Quanto tempo leva para cair? Qual a sua velocidade ao atingir o chão?
ESCOLHA DO EIXO USUAL (Figura 1):
Figura 1:
3
1
x(t) = |{z}
100 + |{z}
v0 t − |{z}
10 t2
2
x
g
(7)
v(t) = v0 −10t
(8)
0
0
|{z}
0
Repare que esta equação faz sentido:
• o x começa em 100 e vai diminuindo. Isto é que significa respeitar o
referencial!
• O vetor aceleração aponta contra o sentido do eixo.
Ao cair no chão
0 = 100 − 5t2 ⇒ t =
√
tqueda = 20 s
4
√
20
(9)
Outra escolha (a da direção da gravidade)(Figura 2):
Figura 2:
x(t) = 100 + 5t2
v(t) = 10t
0 = 100 + 5t2 ⇒ tqueda =
5
(10)
√
(11)
20s
(12)
Outras escolhas (Figura 3)
Figura 3:
1
(1) x(t) = − 10t2 (x0 = 0 estamos na origem)
2
(13)
v(t) = −10t
(14)
1
(2) x(t) = + 10t2 (x0 = 0 estamos na origem)
2
v(t) = +10t
(15)
(16)
NOTE QUE AGORA O CHÃO DE ACORDO COM ESSE REFERENCIAL será localizado a
(1) −100 = − 12 10t2 ⇒ tq =
(2) +100 = + 12 10t2 ⇒ tq =
√
√
20
20
6
ENTENDEU? Exercı́cio para Discussão
3. Então repita tudo para um lançamento vertical. Use
Encontre as equações de movimento nos três casos. Calcule a altura
máxima nos três casos.
7
4. Suponha que você vai fazer uma longa jornada de bicicleta. Na primeira hora você anda 8 km por hora. Depois 4 horas a 21 km/h. Quantas
milhas você andou?
Faça um gráfico. Lembre-se que se tivéssemos incluı́do mais trechos o
cálculo ficaria complicado!
Agora some as áreas. Este exercı́cio é muito simples e será um dos únicos
resolvidos até o fim.
Apredizado esperado: Aprender a esquematizar problemas (quando possı́vel)
na forma gráfica. Não esquecer ou confundir os eixos. Se você tiver gráficos
que já venham com eixos a primeira coisa é ler os eixos e descobrir do que se
trata o problema.
8
5. Abandonando um corpo de certa altura, obtivemos os seguintes dados
para as distâncias percorridas após 1 s, 2 s e 3 s de queda
t(s) 1
d(m) 5
2 3
20 45
Podemos dizer que a distância percorrida d é proporcional ao tempo de
queda, como no movimento uniforme? Faça o gráfico desse movimento e
comente.
6. O gráfico de um movimento retilı́neo uniforme é do tipo
x(t) = a + bt,
(17)
a e b são constantes (x = x0 + vt).
O significado da tangente é a velocidade, que é constante. Faça agora
você o gráfico da velocidade e aceleração correspondentes a esse.
9
7. O movimento uniformemente acelerado tem as seguintes equações de
movimento, num caso especı́fico
1
x(t) = x0 + v0 t + at2
2
(18)
x(t) = 5t + t2
(19)
v(t) = v0 + at
(20)
a(t) = a
(21)
Use
Descubra os valores de x0 , v0 e a. Faça os gráficos de x(t), v(t) e a(t).
Discuta o movimento a partir dos gráficos.
8. Representando as equações de movimentos uniformemente variados
1
x(t) = x0 + v0 t + at2
2
(gráfico de uma parábola)
10
(22)
11
Agora interprete
e construa os outros dois gráficos de acordo. Observe os sinais.
12
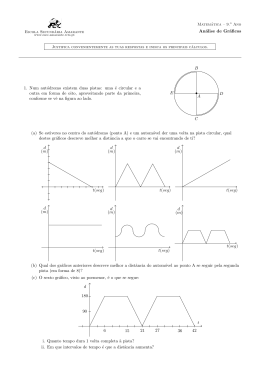
9. Considere o gráfico da velocidade escalar de um móvel em função do
tempo. Determine para que valores do tempo o movimento é
(a) Progressivo
(b) Retrógrado
(c) Acelerado
(d) Retardado
13
10. O gráfico ilustra a distância s em função do tempo t no qual um som
é produzido por uma pessoa atinge um obstáculo e, após reflexão, retorna ao
local onde a pessoa se encontra. A distância do obstáculo à pessoa e o valor
da velocidade da propagação do som valem, respectivamente
14
11. Olhe para o gráfico de velocidades abaixo e apenas responda as
questões lendo as mesmas.
(a) Após 2 horas de viagem, qual a velocidade do móvel?
(b) Quanto (em km) o móvel percorreu durante toda a viagem?
PS: Aprendeu a usar o gráfico?
15
Agora você vai FAZER um
12. Um motorista começa do repouso e acelera a 30 km/h em 10 segundos.
Qual a distância percorrida nestes 10 segundos? Desenhe o gráfico.
16
13. O motorista de um carro A, vendo o sinal verde do semáfaro, arranca com seu carro. Neste instante, um outro carro B passa por ele e ambos
passam a se movimentar em trajetórias paralelas ao longo de uma extensa
avenida.
O gráfico acima mostra a variação de velocidade de ambos os carros desde
o instante em que A começa a se movimentar até 15 s após. Das afirmações
abaixo assinale as verdadeiras
(a) O carro A alcança B depois em t = 3,75 s.
(b) No intervalo 0 - 15 s o carro A não alcança B.
(c) Quando os velocı́metros marcam a mesma velocidade A está cerca de 28
m na frente de B.
(d) Em t = 15 s o carro A está a 25 m à frente de B.
(e) O carro A ultrapassa B em 5 s.
Quando os 2 carros tem a mesma velocidade (v = 3,75 s) o carro B está
na frente do carro A.
17
14. O gráfico abaixo representa o comprimento L de uma mola em função
da massa M aplicada na mesma extremidade da mesma
Determine:
(a) O comprimento inicial do modo (L0 ).
(b) A constante de proporcionalidade entre ∆L e ∆M .
(c) O comprimento de mola para uma massa de 100 g.
(d) Será que essa mola pode fornecer um valor de alongamento para qualquer
valor de massa? Justifique.
18
15. Pote de Moscas. Um grupo de moscas é capiturado em um pote
de vidro. O pote é colocado sobre uma balança. A balança irá registrar o
maior peso quando as moscas estão
(a) pousadas no fundo do pote
(b) voando dentro do pote
(c) ...o peso do pote é o mesmo em ambos os casos.
19
16. A favor do vento. Todo mundo adora um barco a vela, especialmente em dia de vento. Suponha que você está velejando diretamente a
favor do vento com suas velas cheias em um vento de 20 mph (milhas por
hora). Então a velocidade máxima que você espera poder atingir seria
(a) próximo a 20 mph
(b) entre 20 e 40 mph
(c)... não existiria velocidade limite teórica neste caso.
20
17. Cruzando o vento. Mantendo um ângulo menor do que 90o entre
a vela e a quilha do barco, suponha que você direciona seu barco tal que ele
veleja cruzando o vento, ao invés de a favor do vento. O seu barco irá velejar
mais rápido ou mais lento do que antes?
(a) Mais rápido
(b) Mais lento
(c) O mesmo
21
18. Contra o vento. Esta questão é para empregar o conhecimento das
questões anteriores. Para os quatro barcos mostrados observe a orientação
das velas com relação a ambas direções do vento e da quilha. Qual destes
barcos move-se para frente com a maior velocidade?
22
19. Homem forte. Quando um homem forte suspende uma livro de
10 lb (libras) verticalmente com um uma corda a tensão em cada extremidade da corda é de 5 lb. Se o homem consegue suspender o livro comm as
extremidades da corda puchadas horizontalmente como mostrado, a tensão
em cada extremidade seria
(a) cerca de 5 lb
(b) Cerca de 10 lb
(c) Cerca de 20 lb
(d) mais do que um milhão de libras
Referência: Lewis Carroll Epstein ”Thinking Physics is Gedanken Physics”Third Edition, Insight Press, San Francisco, 2005.
23