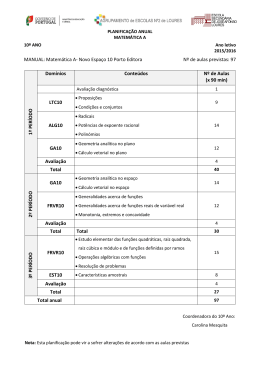
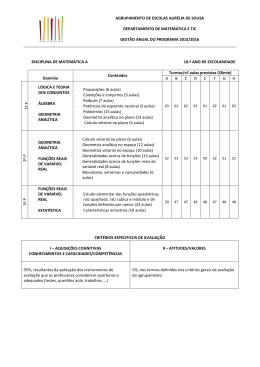
AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500
Planificação Anual /Critérios de avaliação
Disciplina: Matemática A – 10º ano
2014/2015
Início
Fim
Nº de aulas previstas (45’)
1º Período
15 de setembro de 2014
16 de dezembro 2014
76
2º Período
5 de janeiro de 2015
20 de março de 2015
60
3º Período
7 de abril de 2015
12 de junho de 2015
54
TOTAL
190
1º Período
Temas
Número de aulas*
Módulo inicial ( revisão de conceitos do 3º Ciclo )
8
Módulo inicial ( resolução de problemas )
10
Geometria no Plano e no Espaço I
46
2º Período
Temas
Número de aulas*
Geometria no Plano e no Espaço I
10
Funções e gráficos
40
3º Período
Temas
Número de aulas*
Funções e Gráficos
24
Estatística
20
Nota: * Nesta planificação a aula tem a duração de 45 minutos (segmento);
- No 1º período estão contempladas 12 aulas para apresentação/revisões/testes/correções;
- No 2º período estão contempladas 10 aulas para revisões/testes/correções;
- No 3º período estão contempladas 10 aulas para revisões/testes/correções.
Domínio
(Unidade/
tema)
(1)
Subdomínio/conteúdos
Meta de aprendizagem geral
Tempo/
Calendarização
Estratégias/
recursos
Avaliação :
instrumentos/
pesos
Raciocínio matemático
Capacidades
transversais
Comunicação matemática
Ao longo do ano
Conceitos de Lógica Matemática
Síntese de conceitos fundamentais do 3º Ciclo
Resolução de problemas que envolvem a
revisão de temas como simetrias, semelhanças
e outros temas geométricos
Módulo inicial
Resolução de problemas de geometria no
plano e no espaço
Resolução de problemas numéricos
envolvendo números racionais ou irracionais
Resolução de problemas que se traduzem em
equações do 1º ou do 2º graus e interpretar a
ou as soluções
- Testes escritos 80%
-Manual em
suporte físico
ou digital
Rever, aprofundar e consolidar conhecimentos . Calcular
áreas e volumes por decomposição de figuras planas ou
sólidos
Resolver problemas que propiciem o raciocínio matemático,
em particular o raciocínio geométrico
Resolver problemas de Geometria no plano e no espaço
18 tempos de 45’
(1.º período)
Estabelecer conexões entre diferentes domínios da
Matemática e entre esta e a vida real
-Fichas de
trabalho
-Materiais
manipuláveis
- Participação na
aula (questões de
aula, fichas de
trabalho,
participação oral,
caderno diário,
portfólio) - 15%
Aperfeiçoar o espírito crítico e melhorar a confiança nos seus
raciocínios
GAVE
Sólidos geométricos e suas propriedades.
Planificações. Relação de Euler
Perspetiva cavaleira.
Geometria no
Plano e no
Espaço
Número de ouro. Operações com radicais.
Secções determinadas num cubo por um plano
Referencial cartesiano e coordenadas no
plano. Simetrias
Condições e conjuntos de pontos no plano.
Rever e aprofundar conhecimentos de Geometria no Plano e
no Espaço, apoiando-se em figuras planas ou em sólidos que
o aluno vai construir em colaboração com os colegas.
Exercitar o raciocínio espacial e a intuição geométrica, bem
como a capacidade de conjeturar.
Identificar e representar secções produzidas por planos em
sólidos.
Utilizar referenciais no plano e no espaço.
Resolver problemas geométricos no plano e no espaço
Traduzir analiticamente relações entre figuras do plano e do
-Tarefas de
exploração
64 tempos de 45’
(1.º período)
10 tempos de 45’
(2.º período)
-Software
específico
- Atitudes e
Valores
(assiduidade,
pontualidade,
comportamento,
cumprimento de
regras e prazos,
realização dos
trabalhos de casa,
respeitar os colegas
e o professor) –5%
espaço.
Distância entre dois pontos no plano
Usar vetores livres no plano e no espaço.
Estudo de alguns lugares geométricos:
Mediatriz, Circunferência e Círculo.
Usar o método cartesiano para representar : retas, planos
paralelos aos eixos coordenados,planos paralelos aos planos
coordenados, circunferência/ superfície esférica,
mediatriz/plano mediador paralelismo e perpendicularidade
de retas e planos
Domínios planos.
Referencial cartesiano e coordenadas no
espaço. Simetrias.
Condições e conjuntos de pontos no espaço..
Distância entre dois pontos no espaço.
Utilizar os vetores em referencial ortonormados como
instrumento para a resolução de problemas.
Extensão ao espaço tridimensional
Estudo de alguns lugares geométricos: Plano
Mediador, Superfície Esférica e Esfera
Geometria analitica vetorial.
Generalidades sobre funções
Estudo intuitivo de funções e gráficos.
Ampliar os conhecimentos sobre funções, nas vertentes
analítica, numérica e gráfica.I
Estudar a função afim.
Estudar a função quadrática
Funções e
gráficos
Identificar o domínio e o contradomínio, zeros, sinal,varição,
extremos, injetividade e paridade de funções dadas gráfica
ou analiticamente.
Estudar a função módulo.
Transformações simples de funções
Polinómios – Generalidades
Operações com polinómios. Regra de Ruffini.
Divisibilidade por x  
Decomposição em fatores.
Compreender a importância de algumas funções,
nomeadamente as funções polinomiais e as funções
definidas por ramos,.
Resolver equações e inequações por métodos numéricos e
gráficos, nomeadamente as que resultam de problemas
envolvendo as referidas funções
40 tempos de 45’ (
2.º período )
24 tempos de 45’ (
3º período )
Estudar as funções polinomiais
Equações e inequações de grau maior que 2
Modelação.
Estudar as funções definidas por ramos
Estatística. Generalidades.
Estatística
Organização de dados e interpretação de
carateres estatísticos.
Ampliação do estudo das Medidas de
localização. Medidas de dispersão.
Rever, aprofundar e consolidar conhecimentos de Estatística.
20 tempos de 45’
(3º período)
Interpretar e comparar distribuições estatísticas recorrendo
às medidas de localização e de dispersão e a gráficos.
Distribuições bidimensionais
1)
Cálculo das Classificações finais dos 2º e 3° Períodos:
A avaliação é um processo contínuo e, como tal, a classificação a atribuir no final de cada período terá em consideração a classificação final
do período anterior.
(
Classificação 2º P = Classificação do 1°período x 0,4 + N2 x 0,6
Classificação 3°P = Classificação do 2°período x 0,6 + N3 x 0,4
N2 e N3 são as classificações obtidas de acordo com os critérios de avaliação no 2° e 3° período, respetivamente.
N2 e N3 são valores arredondados às décimas.