8.EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
Parte 3
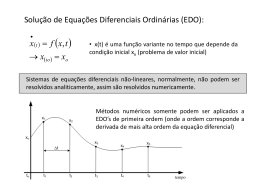
8.1 – INTRODUÇÃO – PVI’s
8.2 – MÉTODOS DE PASSO SIMPLES
8.2.1 – MÉTODO DE EULER
8.2.2 – MÉTODOS DE TAYLOR
8.2.3 – MÉTODOS DE RUNGE-KUTTA
hoje
8.3 – MÉTODOS DE PASSO MÚLTIPLO
8.4 – MÉTODOS PREVISOR-CORRETOR
8.5 – EDO’s DE ORDEM SUPERIOR E SISTEMAS DE EDO’s
8.6 - PVC’s E O MÉTODO DAS DIFERENÇAS FINITAS
8. EDO’s
8.2.3 – Métodos de Runge-Kutta
 Vimos os métodos de Euler, Euler
Inverso e Euler Aprimorado para
resolver problemas de valores
iniciais (PVI’s)
y   f x, y 
com yx0   y 0
 Estes métodos são classes de métodos de Runge-Kutta como veremos.
8. EDO’s
8.2.3 – Métodos de Runge-Kutta
 Carl David Runge (1856-1927) Físico alemão – Trabalho de 1895
sob soluções numéricas de EDO’s.
 M. Wilhelm Kutta (1867-1944) –
Matemático alemão – Aprimorou o
método em 1901 ao estudar
aerodinâmica se aerofólios.
8. EDO’s
8.2.3 – Métodos de Runge-Kutta
 A idéia dos métodos que estudaremos
é aproveitar as qualidades dos métodos das séries de Taylor eliminando o
seu maior defeito que é o cálculo de
derivadas de f(x,y).
 Os métodos de Runge-Kutta de ordem
p caracterizam-se pelas propriedades:
1- São métodos de passo um;
2- Não calculam derivadas;
3- Em mesma ordem, as fórmulas de
Taylor e Runge-Kutta são semelhantes.
8. EDO’s
8.2.3 – Runge-Kutta de 1ª ordem
 O método de Runge-Kutta de 1ª ordem
é o método de Euler ou de Taylor de 1ª
ordem:
 yn1  yn  f xn ,yn  h
onde

xn 1
xn
(1)
f x, y dx  h f [ xn ,yn ] .
Note que (1) satisfaz as três porpriedades
dos métodos de Runge-Kutta.
8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 Os métodos de Runge-Kutta de 2ª ordem devem ter fórmulas que devem
ser semelhantes às fórmulas do Método de Taylor até termos de segunda
ordem em h.
 Consideremos o método de Euler
aprimorado ou fórmula de Heun
y n 1
f xn , y n   f xn 1 , y n 1 
 yn 
h
2
(2)
8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 Reescrevendo a fórmula de Heun
y n 1
h
 yn 
2
 f xn ,yn 
 f x n  h , y n  h y n  
(2)
1- Observando que para calcular yn1  yxn1 
usamos apenas yn  yxn  , então dizemos que o Método de Euler Aprimorado é
de Passo Um ou de Passo Simples.
2- O Método de Euler Aprimorado não
tem derivadas de f(x,y).
3- Resta verificar a terceira condição.
8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 Resta verificar se a fórmula de Heun
y n 1
h
 yn 
2
 f xn ,yn 
 f x n  h , y n  h y n  
(2)
é semelhantes às fórmulas do Método de Taylor
até termos de segunda ordem em h. Da fórmula
de Taylor de y(x) em x=xn+1
h2
y ( x n 1 )  y ( x n )  y ( x n ) h  y ( x n )
2!
h2
 y n 1  y n  y n h  y n
2!
8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 Calculemos a fórmula de Taylor de 2ª ordem.
y x   f x, y ( x) 
d
dy


y x  
f  x, y ( x )   f x  x, y ( x )   f y  x, y ( x )   f x  f f y
dx
dx
h2
 y n 1  y n  h f x n , y n  
f x xn , y n   f y xn , y n  f xn , y n  
2
h2
erro de truncamento E(xn 1 ) 
y ()
3!


8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 No Método de Euler Aprimorado trabalhamos
Com f xn  h , yn  h yn.
Expandindo f  x, y ( x)  em t ornode (x n , y n )
 f ( x, y )  f ( x n , y n )  f x  x n , y n  x  x n   f y  x n , y n   y  y n  
1
1
2
2
 f xx ,   x  x n   f yy ,    y  y n 
2
2
 f xy ,   x  x n  y  y n  
com    x, x n  e    y, y n 
8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 Segue que:
f (x n  h, y n  h y n )  f ( xn , y n )  f x xn , y n  h  f y xn , y n  h y n 


h2
2

f xx ,   2 f xy ,   y n   f yy ,   y n 
2
e o Método de Euler Aprimorado escreve-se
h
 f xn ,yn   f xn  h , y n  h y n  
y n 1  y n 
2
h
 y n  { f  x n ,yn  f ( xn , y n )  f x xn , y n  h  f y xn , y n  h y n 
2
2
h
2

f xx ,   2 f xy ,   y n   f yy ,   y n  }
2


8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
Enfim
y n 1


h2
 y n  h f ( xn , y n ) 
f x xn , y n   f ( xn , y n ) f y xn , y n  
2
h3

f xx ,   2 f ( x n , y n ) f xy ,   f 2 ( x n , y n ) f yy , 
2

Logo, o Método de Euler Aprimorado é um
método de Taylor de 2ª ordem e portanto,
devido às 3 propriedades verificadas, também
é um Método de Runge-Kutta de 2ª ordem.

8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 A Fórmula geral de Runge-Kutta de 2ª ordem
tem a forma:
yn1  yn  h a1 f ( xn , yn )  h a2 f xn  b1h , yn  b2 h yn 
 No caso do Euler Aprimorado
a1 
1
1
, a 2  , b1  b2  1
2
2
(3)
8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
 Questão: A expressão (3) sempre é semelhante a fórmula de Taylor com termos até
segunda ordem em h?
yn1  yn  h a1 f ( xn , yn )  h a2 f xn  b1h , yn  b2 h yn 
 Realizando um procedimento semelhante
àquele realizado para o Método de Euler
Aprimorado, verificamos que os parâmetos
devem ser tais que
1
1
a1  a 2 1 , a 2 b1  , a 2 b2 
2
2
(3)
8. EDO’s
8.2.3 – Runge-Kutta de 2ª ordem
Como temos um parâmetro arbitrário, tomamos,
por exemplo,
1
a 2  w  a1  1  w , b1  b2 
2w
de modo que a fórmula de Runge-Kutta de 2ª
ordem escreve-se como:
y n1
h
h


 y n  h 1  w f ( xn , y n )  h w f  xn 
, yn 
f ( xn , y n ) 
2w
2w


8. EDO’s
8.2.3 – Runge-Kutta de 3ª ordem
De forma análoga podemos construir a fórmula
de métodos de Runge-Kutta de 3ª ordem. Sejam
PVI’s do tipo y   f x, y  com yx0   y 0
então uma fórmula de Runge-Kutta de 3ª ordem
escreve-se como:
y n 1

h
 yn 
2 K1  3 K 2  4 K 3
9


K1 
h


onde K 1  f ( x n , y n )
K 2  f  xn  , y n 
2
2 


3K 2 
3h


K 3  f  xn 
, yn 
4
4 

8. EDO’s
8.2.3 – Runge-Kutta de 4ª ordem
De forma análoga podemos construir a fórmula
de métodos de Runge-Kutta de 4ª ordem. Sejam
PVI’s do tipo y   f x, y  com yx0   y 0
então uma fórmula de Runge-Kutta de 4ª ordem
escreve-se como:
y n 1

h
 y n  K1  2 K 2  2 K 3  K 4
6
onde
K1  f ( xn , y n )
,


K1 
h


K 2  f  xn  , y n 
2
2 


K2 
h

 , K 4  f x n  h , y n  K 3
K 3  f  xn  , y n 
2
2 



8. EDO’s
8.2.3 – Comentários sobre Runge-Kutta
FÓRMULAS DE RUNGE-KUTTA
1ª ordem: yn1  yn  f xn ,yn  h
h
2ª ordem: y n 1  y n   f x n , y n   f x n 1 , y n 1   particular
2
h
h


y n1  y n  h 1  w f ( xn , y n )  h w f  xn 
, yn 
f ( xn , y n ) 
2w
2w


h
3ª ordem: y n1  y n  9 2 K1  3 K 2  4 K 3 


K1 
3K 2
h
3h



K1  f ( x n , y n ) , K 2  f  x n  , y n 
, K 3  f  xn 
, yn 

2
2 
4
4





8. EDO’s
8.2.3 – Comentários sobre Runge-Kutta
FÓRMULAS DE RUNGE-KUTTA
4ª ordem: y n 1

h
 y n  K1  2 K 2  2 K 3  K 4
6
onde
K1  f ( xn , y n )
,


K1 
h


K 2  f  xn  , y n 
2
2 


K2 
h

 , K 4  f x n  h , y n  K 3
K 3  f  xn  , y n 
2
2 


Com1: As fórmulas de Runge-Kutta são médias
ponderadas de valores de f(x,y) em pontos no
intervalo xn  x  xn1 .

8. EDO’s
8.2.3 – Comentários sobre Runge-Kutta
FÓRMULAS DE RUNGE-KUTTA
Com2: As somas


h
K 1  2 K 2  2 K 3  K 4 ; h 2 K 1  3 K 2  4 K 3 
6
9
podem ser interpretadas como um coeficiente angular
médio.
Com3: Problema do passo fixo pode ser resolvido com o
desenvolvimento de Métodos de Runge-Kutta adaptativos,
os quais ajustam o passo de modo a manter o erro de truncamento local num nível de tolerância fixado.
8. EDO’s
8.2.3 – Exemplos de Runge-Kutta
Exemplo 1: Para o PVI dado, estime y(1).
com y(0)  1000
PVI: y   0.04 y
a) Runge-Kutta de primeira ordem.
y n1  y n  f xn ,yn  h
onde f x,y  0.04y
 y n1  y n  0.04 y n h  1  0.04 h y n
Assim
y1  1  0.04 h  1000
y 2  1  0.04 h  y1  1  0.04 h  1000
2
............................................................
y k  1  0.04 h  1000 para k  1,2,3..
k
8. EDO’s
8.2.3 – Exemplos de Runge-Kutta
Definindo a partição do intervalo (0,1)
h  1  y1  1  0.04 1000  1040
h  0.5  y 2  1  0.04 0.5 1000  1040.4
2
h  0.25  y 4  1  0.04 0.25 1000  1040.604
4
h  0.1  y10  1  0.04 0.1 1000  1040.7277
10
Valor exato: y (1)  1040.8108
8. EDO’s
8.2.3 – Exemplos de Runge-Kutta
b) Runge-Kutta de 2ª ordem. Euler aprimorado.
h
y n 1  y n   f  x n , y n   f  x n  h , y n  h f  x n , y n 
2
h
 y n 1  y n  0.04 y n  0.04  y n  h  0.04 y n 
2
h


 y n 1  y n 1  0.04 h   0.042 
2


Analogamente ao Runge-Kutta de 1ª ordem
k
h


y k  1  0.04 h   0.042   1000
2


8. EDO’s
8.2.3 – Exemplos de Runge-Kutta
Definindo a partição do intervalo (0,1)
1


h  1  y1  1  0.04   0.042  1000  1040.8
2


2


0.5
h  0.5  y 2  1  0.04 0.5 
 0.042  1000  1040.808
2


2
4

0.252
2
h  0.25  y 4  1  0.04 0.25 
 0.04  1000  1040.8101
2


10


0.1
h  0.1  y10  1  0.04 0.1 
 0.042  1000  1040.8107
2


Valor exato: y (1)  1040.8108
2
8. EDO’s
8.2.3 – Exemplos de Runge-Kutta
c) Runge-Kutta de 3ª ordem.


h
y n 1  y n 
2 K1  3 K 2  4 K 3
9


K1 
3K 2
h
3h



K1  f ( xn , y n ) , K 2  f  xn  , y n 
, K 3  f  xn 
, yn 

2
2 
4
4




K1 
3K 1 




 K 1  0.04  y n , K 2  0.04   y n 
, K 3  0.04   y n 

2 
4 





8. EDO’s
8.2.3 – Exemplos de Runge-Kutta
c) Runge-Kutta de 3ª ordem.


h
2 K1  3 K 2  4 K 3
9
40 

 K 1  0.04  1000  40 , K 2  0.04  1000   40.8
2 

3


K 3  0.04  1000 40.8   41.224
4


Sendo
y1  y 0 
Logo : y1  1000
1
2  40  3  40.8  4  41.224  1040.8107
9
para h  1
8.2.3. Métodos de Runge-Kutta
Exercícios
Exercício: Utilize o Método de Runge-Kutta de 1ª,
2ª, 3ª e 4ª ordens, para calcular valores
aproximados da solução y(x) do problema de
valor inicial no intervalo [0,2].
y  1  x  4 y
com
y(0)  1
Utilize partições h=0.5 , h=0.25 e h=0.1